之前我们聊了
今天我们满足了所有前置知识,可以来看这篇的本体了。如何把diffusion models 用到可控文本生成中。虽然是老本行,但这篇还是精读一下。
摘要
- 可控文本生成是一个重要的任务
- 已有的方法对粗粒度的控制尚可(情感),但对细粒度的控制效果不好(句法树)
- 本文设计了一个非自回归的、连续的diffusion model来解决这个问题
- 去噪过程中的多个中间量可以指导可控的文本生成过程
- 在6个可控生成任务中,Diffusion-LM模型大幅战胜了SOTA
Introduction
自回归的语言模型的生成能力很强,但可控性很弱。如果想做可控的生成:
- 直观方法是做有监督的训练,但这样需要每个任务炼一个模型,成本高。
- plug-and-play的方法,冻住模型。但此类方法效果差,难以实现细粒度的控制
传统的连续diffusion model不适用于文本,因为word是离散的。本文通过添加一个embedding步骤和一个rounding步骤解决这个问题。同时,本文通过一种可控的gradient update指导模型可以平衡fluency和controllable两种属性。
本文在6个可控任务中大幅战胜plug-and-play SOTA,同时战胜了fine-tune的方法。甚至,在不用classifier的情况下和自回归的模型有的一拼。
Related work
Diffusion Models for Text: 已有方法都是在离散的空间做这件事,提到的论文我也看了,有时间给大家写一篇笔记。本文用了连续的方法来做。
Autoregressive and Non-autoregressive LMs: 已有的模型大多是是从左到右训练的,但是对于infilling等任务来说,这限制了模型的发挥。这个问题,有一些解决方法。本文的diffusion model是classifier指导的,所以可以看到句子的全部。
Plug-and-Play Controllable Generation:冻结模型,训一个类似分类器的东西。已有方法大多基于自回归模型:
- FUDGE:通过对生成质量的估计来reweight LM prediction
- GeDi, DExperts: 通过fine--tune一个小的LM来reweight LM prediction
- GeDi的论文没准后面也写个笔记
PPLM方法和本文最接近,通过一个分类器做梯度上升。但由于是自回归的,只能从左到右,不能实现细粒度的控制。
Problem Statement and Background
Generative Models and Controllable Generation for Text
如何在控制条件c的情况下生成w,最大化\(P(w|c)\).由于 \[ \begin{aligned} P(w|c) & = \frac{P(w)\times P(c|w)}{P(c)} \\ & \propto P(w)\times P(c|w) \end{aligned} \] 如果对w的生成求导: \[ \bigtriangledown_w \log P(w|c) = \bigtriangledown_w \log P(w)+ \bigtriangledown_w \log P(c|w) \] 可以发现,右边是正常模型的输出的梯度,后面是某个分类器的输出的梯度。这个其实就是经典的在图像领域做可控生成的diffusion model的方法
Autoregressive Language Models
\[ P_{lm}(w) = P_{lm}(w_1) \sum_{i=2}^N P_{lm}(w_i| w_{<i}) \]
这是一个经典的从左到右的解码过程。一般大家都是用一个transformer结构来做\(P_{lm}(w)\)
Diffusion Models for Continuous Domains
这一部分是DDPM的子集,可以参考
结论是: \[ \mathcal{L}_{simple} = \sum_{t=1}^T \mathop{\mathbb{E}} \limits_{q(x_t| x_0)} || \mu_\theta(x_t,t) - \hat{\mu}(x_t,x_0)||^2 \\ \hat{\mu}(x_t,x_0) = \text{mean} [q(x_{t−1}|x_0, x_t)] \] 大概就是估计模型对每一个\(x_{t-1}\)都做估计,把估计和实际值的偏差叠加在一起。所谓的"mean"是指后面来自一个高斯分布,这个是期望
Diffusion-LM: Continuous Diffusion Language Modeling
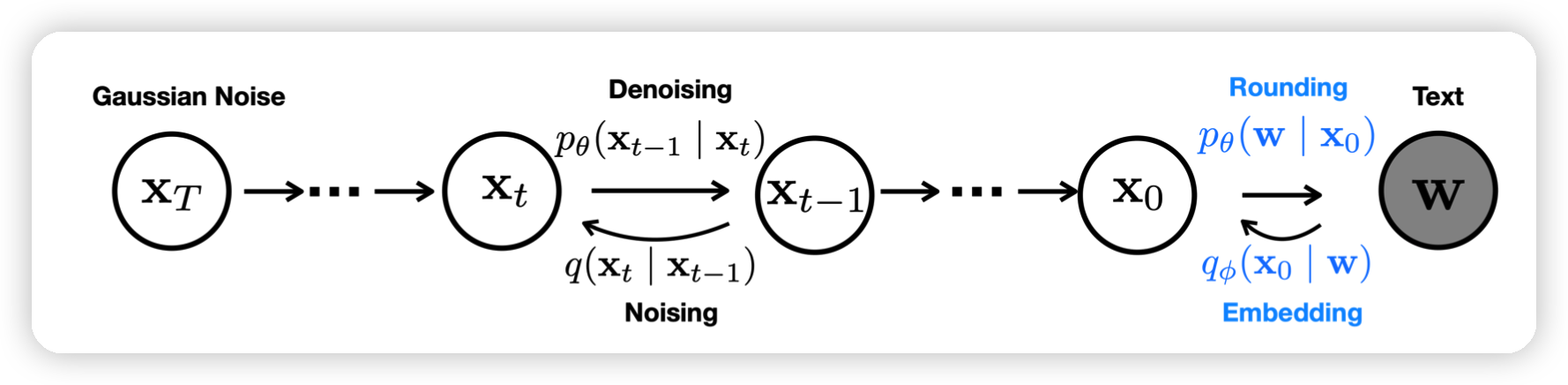
其实这一部分开始才是本文的方法:
- 首先用一个EMB层把离散的word映射到连续空间
- 定义一个端到端的training objectives
- 定义一个rounding method再把生成的连续向量映射回word
- 同时,为了rounding的效果,提出了专门的训练策略
End-to-end Training
\[ EMB(w) = [EMB(w_1), . . . , EMB(w_n)] \in R^{nd}. \]
是一个词向量映射,把n个word映射成n个d维向量,这个是可学习的。
接下来把 \[ q_\phi (x_0|w) = \mathcal{N} (EMB(w), \sigma_0I) \] 视做diffusion process的第一步(其实\(\phi\)就是embedding层模型……)
此外,添加rounding过程 \[ p_\theta(w | x_0) = \sum^n_{i=1} p_\theta(w_i | x_i) \] \(p_\theta(w_i | x_i)\)就是一个经典的softmax变换。
最后: \[ \begin{aligned} \mathcal{L}_{vlb}(x_0) & = \mathbb{E}{(x_0\sim p_{data})} [\log p_\theta (x_0 )] \\ & = \mathop{\mathbb{E}}\limits_{x_{1:T}|x_0} \left[ \log \frac{P_\theta(x_T | x_0)}{P_\theta (x_T)} + \sum_{t=2}^T \log \frac{q(x_{t−1}|x_0, x_t)}{P_\theta(x_{t-1} | x_t)} -\log P_\theta(x_{0} | x_1) \right] \end{aligned} \]
\[ \begin{aligned} \mathcal{L}_{vlb}^{e2e}(w) & = \mathop{\mathbb{E}}\limits_{x_0|w}\left[\mathcal{L}_{vlb}(x_0) +\log q_\phi(x_0 | w) - \log p_\theta(w | x_0) \right] \\ & = \mathop{\mathbb{E}}\limits_{x_{0:T}|w} \left[ \mathcal{L}_{simple}(x_0) + ||EMB(w)−\mu_\theta (x_1 ,1) ||^2 -\log p_\theta(w | x_0) \right] \end{aligned} \]
这是一个端到端的训练loss。只需要给出很多w,用DDPM的算法,就可以慢慢让模型学习了。作者也发现,这样模型和embedding一起学出来,最后word embedding也可以表现出一定的聚合性

Reducing Rounding Errors
rounding的过程其实是对每一个位置选取最接近的embedding。
作者提到,如果像一般的DDPM那样用模型预测$p_(x_{t−1} | x_t) $的均值,会导致输入长度很短的时候效果很差(图像领域没出问题,因为最短也是32x32)。
解决办法是用模型直接预测\(x_0\). \[ \mathcal{L}_{x0-simple}^{e2e}(x_0) = \sum_{t=1}^T \mathbb{E}_{x_t} ||f_\theta(x_t,t) - x_0||^2\\ f_\theta(x_t,t) \to x_0 \] 这里有点怪:换模型的目标好像会影响sample方法?还是说同样是预测\(x_{t-1}\),但是把\(x_0\)视为\(x_{t-1},x_t\)的线性组合
这样模型可以很快发现\(x_0\)的每一个位置都应该对应某个word的embedding。
同时,修改原来的sample方法: \[ x_{t−1} =\sqrt{\overline{\alpha}}f_\theta(x_t,t)+ \sqrt{1- \overline{\alpha}} \epsilon \\ \overline{\alpha} = \sum_{s=0}^t (1 -\beta_t) ,\quad \epsilon \sim \mathcal{N}(0,I) \] (能成立是因为连续的高斯采样等价于从最开始只做一次高斯采样)
上面的方法随着t的递减,逐渐从随机噪声恢复成一个无噪音的数据
如果希望模型可以显式地对齐某个embedding,可以在每一步都加一个clamp。取和\(f_\theta(x_t,t)\)最接近的word embedding \[ x_{t−1} =\sqrt{\overline{\alpha}} \text{Clamp}(f_\theta(x_t,t))+ \sqrt{1- \overline{\alpha}} \epsilon \] 同时作者也提到,对于t很大时做clamp是一个负优化,因为这时\[f_\theta(x_t,t)\]还没有对应到某些embedding,因此选取clamp的开始时间是一个超参。
Decoding and Controllable Generation with Diffusion-LM
Controllable Text Generation
正如前面提到的: \[ \bigtriangledown_{x_{t-1}} \log P(x_{t-1}|x_t,c) = \bigtriangledown_{x_{t-1}} \log P(x_{t-1} | x_t)+ \bigtriangledown_{x_{t-1}} \log P(c|x_{t-1}) \] 其中式子右边的第一项是Diffusion-LM的输出。右边是一种分类器的输出。如果对于目标任务,我们在目标数据集训练一个分类器,在sample时每一步都根据这个输出做更新,那么最终就会生成符合条件c的结果。
同时作者为了细粒度的控制”可控性“,定义一个超参\(\lambda\)来平衡流畅度和控制程度 \[ p(x_{t−1} | x_t, c) = \lambda \log P(x_{t-1} | x_t)+\log P(c|x_{t-1}) \] 作为最终用来指导梯度的东西。作者提到每次得到\(x_t\)之后:
sample \(x_{t-1}\)
再做三轮Adagrad更新
把sample步骤从2000步变成200步来加速
这个方法我理解类似于之前微分方程那篇文章提到的PC更新方式
Minimum Bayes Risk Decoding
这个方法可以得到一个高质量的结果。作者用下面的最小化risk函数: \[ \hat{w} = \mathop{\text{argmin}}_{w \in S} \sum_{w' \in S} \frac{1}{|S|} \mathcal{L}_{bleu}(w,w') \] 这种方法可以参考 MBR解码博客
Experimental Setup
作者在很多个任务上使用了Diffusion-LM方法:
- classifier-guided
- classifier-free:不需要分类器,比如说句子长度。只要最开始的初始化向量变成需要长度即可(控制率显然是100%)
Diffusion model里面的内部解码层作者使用了一个非常传统的transformer结构,80M参数,可以说是很少:
- 步骤T = 2000
- 词向量维度 d = 16-128
- 句长n=64

输入就像上图input所示:通过分类器来在解码中每一次去噪都提供梯度
Result
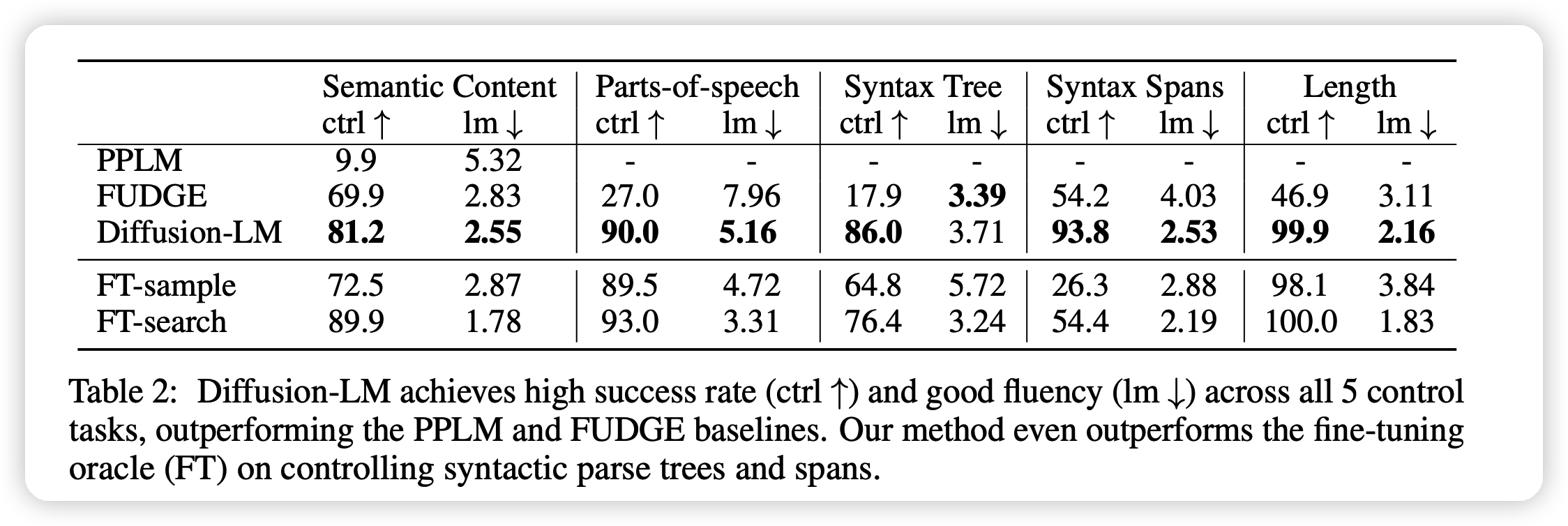
主要结果就如上图所示。
- 基本上把SOTA得分翻倍了,但这个SOTA是指plug-and-play的方法
- 在Syntax Tree, Syntax Spans任务上,甚至比fine-tune的模型效果还好
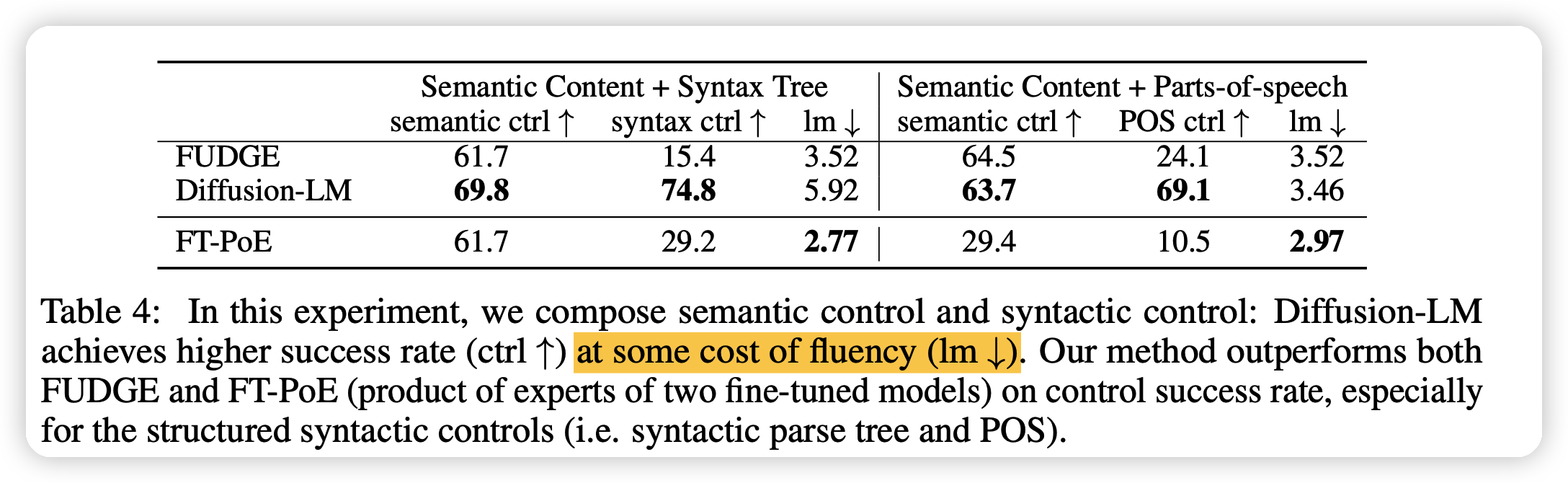
同时作者也做了综合的控制实验,比如说同时限定两个条件。可以看出,效果很好,方法就是单纯的把控制的梯度转换成两个classifier梯度的综合。

在infilling任务中,Diffusion-LM在没有做额外训练的情况下就表现很好
我的思考
这篇工作很新颖,很有启发,我觉得可以做的点还有以下两个方面:
- 这个方法好像不能实现平行的转换,只能”根据某些控制生成特定的句子“。像之前DALL.E都是可以把特定的句子翻译成对应的图像。
- 感觉短文本领域,只有更加平行,才能更加泛用。不过在长文本领域,可能这种没有平行的生成会更好,但作者并没有测试。