这篇论文探索了DDPM对于NLL指标效果不好的原因,并且从实际训练的角度给出了很多可行的改进。

这篇论文是21年的NIPS,作者来自OpenAI,其实就是后面GLIDE的作者。我理解大概是OpenAI看到了DDPM的论文,然后用”财大气粗“的方式来了一波复现和改进。这篇论文其实更偏向于分析性文章。另外,这篇论文的方法的代码和复现性很好。 > 发现一个讲IDDPM代码的是视频
本文大概探索了这个几个问题:
- DDPM的训练object
- \(\beta_t\)的选取
- 训练的采样方法
- DDPM模型的可扩展性
Denoising Diffusion Probabilistic Models
这里重新梳理了一遍DDPM,我就说几个新颖的地方
Definition
作者写出了\(L_{VLB}\)的形式
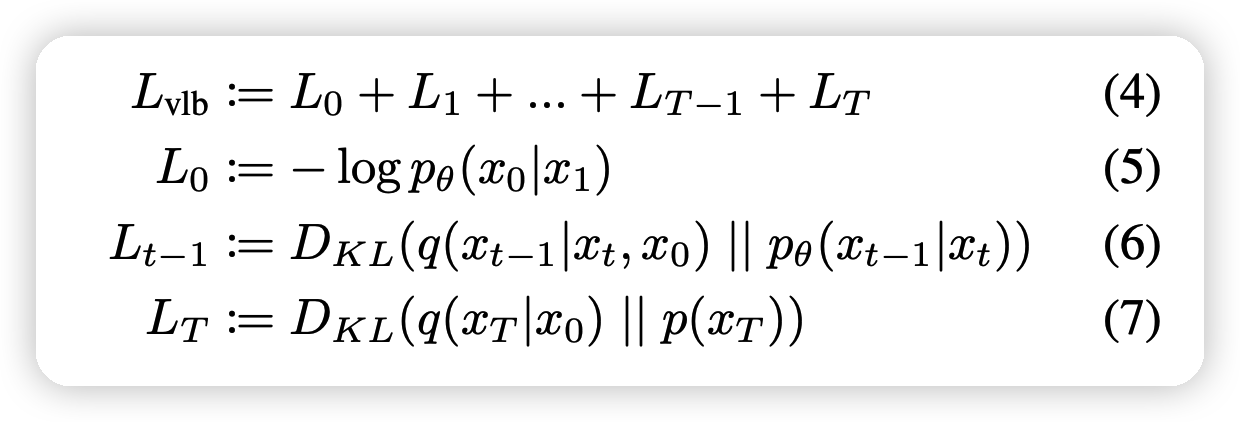
可以看出中间的项都是KL散度,可以通过前后两个高斯分布的均值和方差直接计算出来:
- 正常的DDPM模型\(p_\theta\)模型的均值由模型得出,而方差是确定性的
- \(q(x_{t-1} | x_t, x_0)\)的均值方差均可以被代数表示
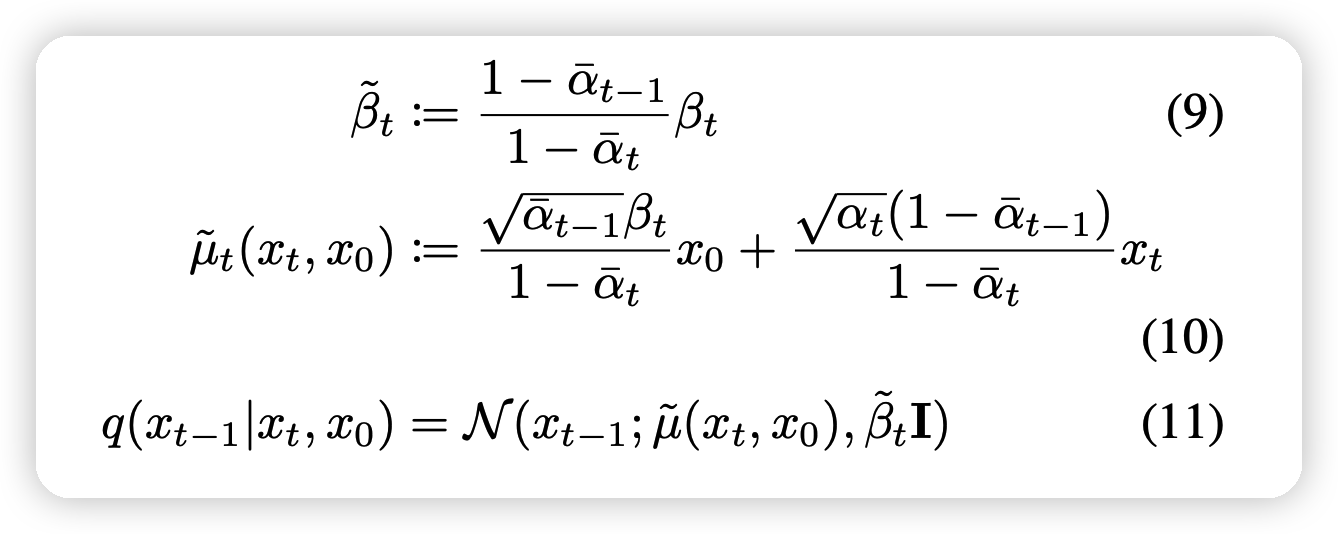
Training in Practice
这一部分,作者说到了三种模型目标:
- 生成 \(\mu_\theta(x_t,t)\),预测\(x_{t-1}\)的均值
- 预测\(x_0\),采样时根据公式10线性拟合出\(x_{t-1}\)进行去噪
- 预测加噪时的噪声\(\epsilon\),去噪根据下式和公式10拟合出\(x_{t-1}\)
\[ x_0 = \frac{1}{\sqrt{\alpha_t}}\left( x_t - \frac{\beta_t}{\sqrt{1 - \overline{\alpha}_t}} \epsilon \right) \]
DDPM在训练过程中使用最后一种,表现最好
作者把\(L_{VLB}\)进行了一波reweight,得出下式作为训练loss进行训练 \[ L_{\text{simple}} = \mathbb{E}_{t,x_0,\epsilon} || \epsilon - \epsilon_\theta(x_t,t)||^2 \]
同时,作者说到在predict阶段,使用下面两种方差效果很接近
- \(\sigma_t^2 = \beta_t\)
- \(\sigma_t^2 = \tilde\beta_t\)
Improving the Log-likelihood
这里作者提到Log-likelihood这个指标在图像生成也很重要,但DDPM在这个指标的效果不好(虽然FID不错)。
learning \(\Sigma_\theta(x_t,t)\)
作者思考为什么DDPM的两个方差效果接近
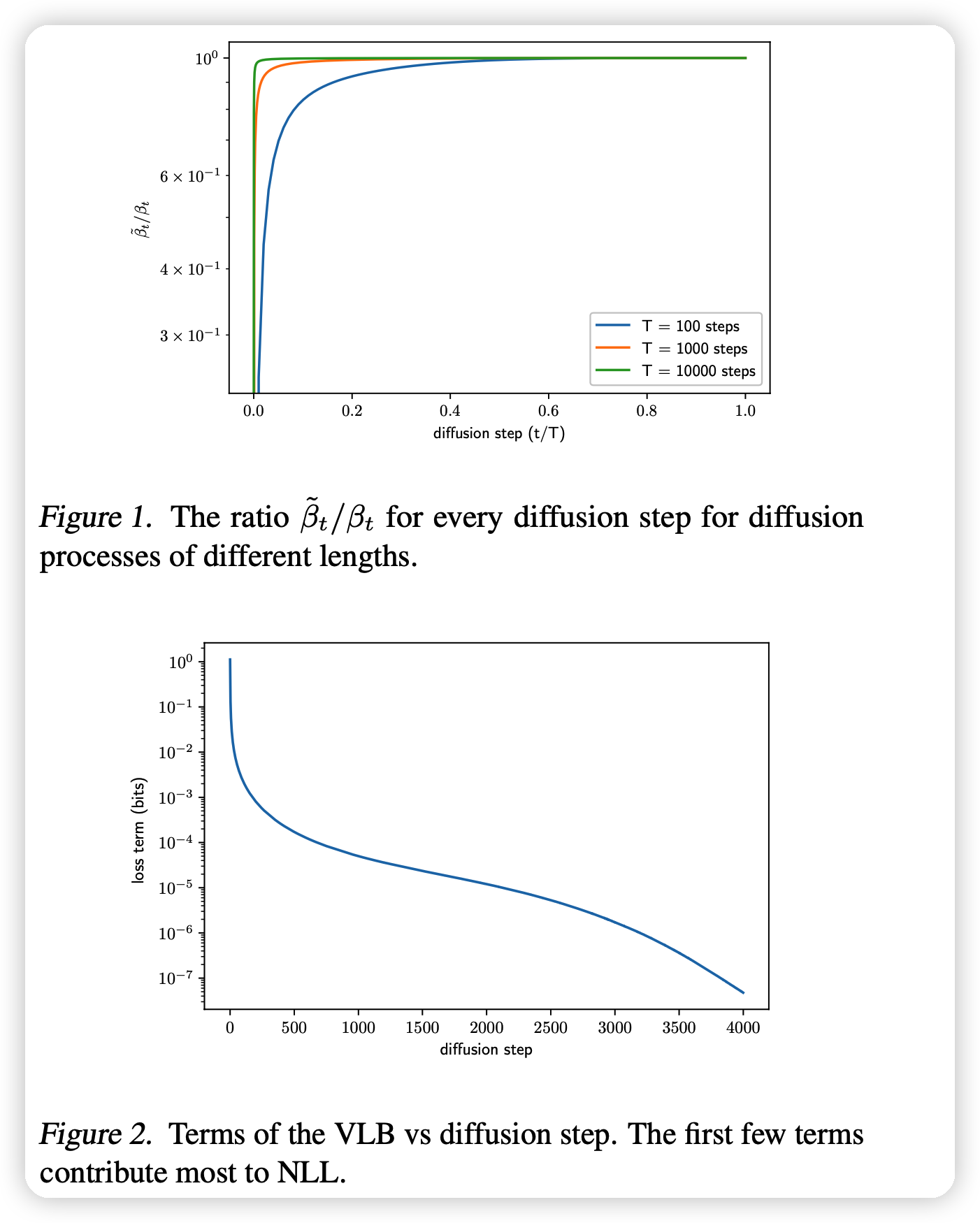
图一可以发现两种方差只在\(t\)很小的时候有差距,别的时候基本一致
图二可以发现\(t\)小的时候对NLL的影响是最大的
综合上面观点,作者觉得NLL效果差的重要原因就是对方差的估计有偏差(上面两种\(\sigma\)都是估计的形式)。因此作者想要找到更好的方差,作者希望通过网络拟合它,看做两种\(\sigma\)的拟合 \[ \Sigma_\theta(x_t,t) = \exp (v \log \beta_t + (1-v)\log \tilde\beta_t) \] 其中v是可学习的参数。作者在这里没有对v的范围做限制,但实际训练还是控制在0-1内。说明DDPM作者选取的两个估计还是很靠谱的
想要学习这个v,就只能把loss直接表示成\(L_{VLB}\),才能反向传播到v,因此作者选择了最终的loss函数 \[ L_{\text{hybird}} = L_{\text{simple}} + \lambda·L_{VLB} \] 其中\(\lambda=0.001\)
Improving the Noise Schedule
这一部分,作者探索了\(\beta\)的选取
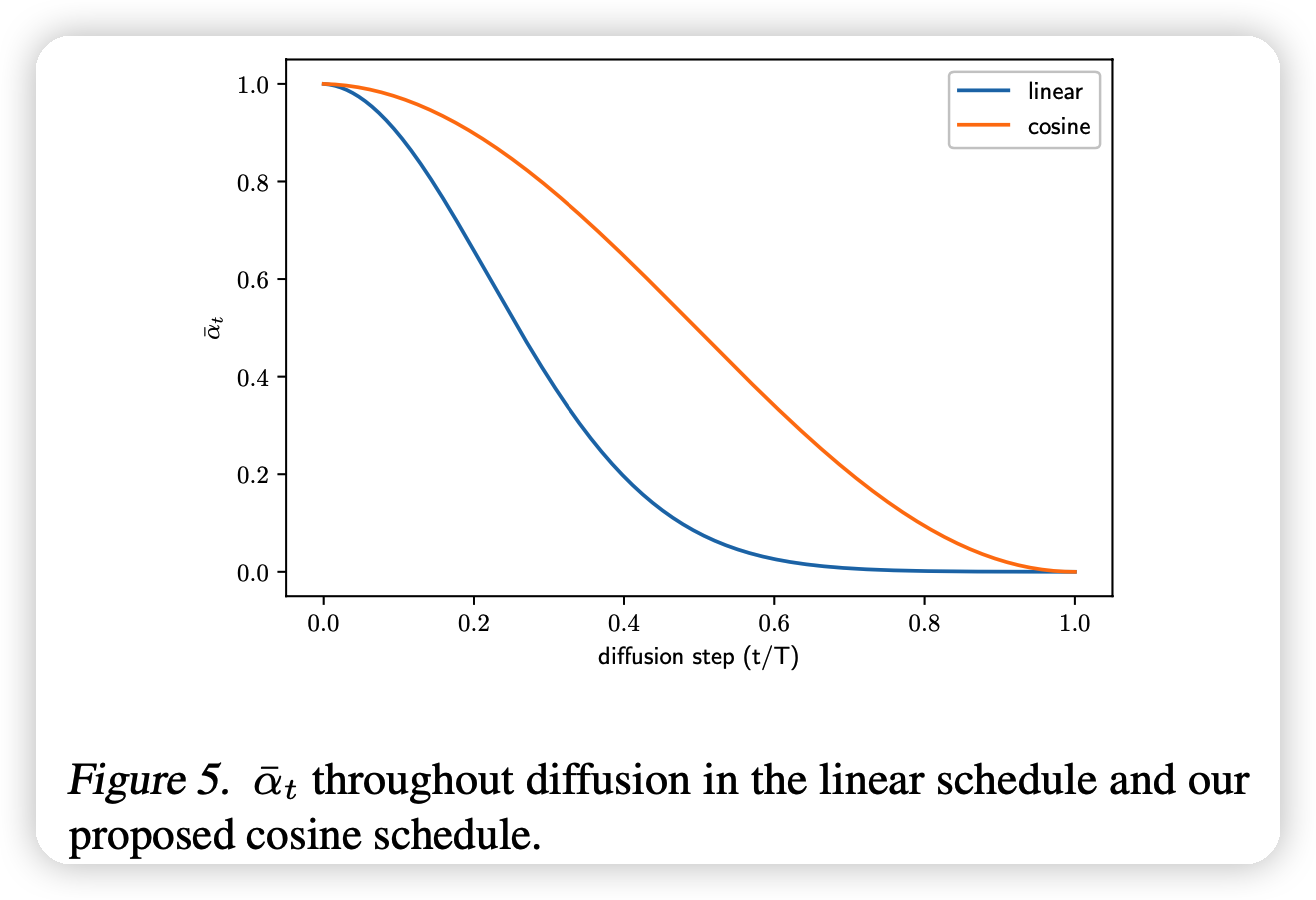
DDPM使用linear来选取,作者采用新的cosine的公式选取 \[ \overline\alpha_t = \frac{f(t)}{f(0)},\quad f(t) = \cos \left(\frac{t/T + s}{1+s}·\frac{\pi}{2} \right)^2 \\ \beta_t = \min(0.999,1 - \frac{\overline\alpha_t}{\overline\alpha_{t-1}}) \] 这中选取方式比linear更稳定。同时作者指出,类似cosine的这种形状的,最后效果都差不多
Reducing Gradient Noise
第三个改进是让训练更稳定
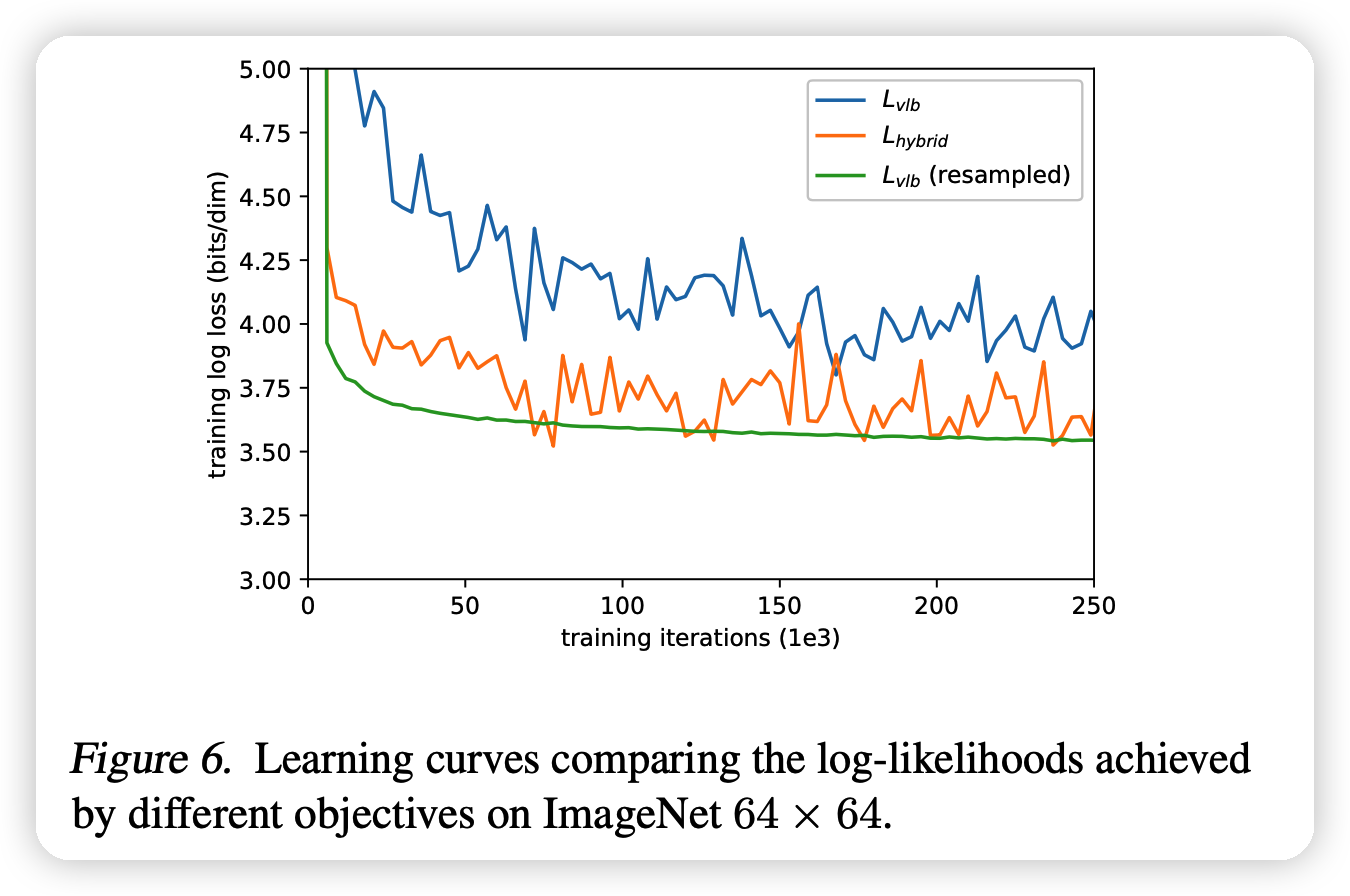
作者发现直接优化\(L_{VLB}\)的训练非常不稳定,比起优化\(L_{simple}\)。作者发现这是由于\(L_{VLB}\)参数对梯度更分散。
进一步分析,发现是在训练时平均的选取t导致训练额外的噪声,实际上的选取应该是: \[ L_{VLB} = \mathbb{E}_{t \sim p(t)} \left[ \frac{L_t}{p_t} \right], \text{where}\quad p_t \propto \sqrt{\mathbb{E}[L_t^2]}, \quad \sum p_t = 1 \] 对于每个t,在训练过程中都可以维护\(L_t\),只要训练开始一段时间以后。
- 先平均选取t,直到每个t都有10个\(L_t\)的历史数据为止
- 接下来,按照前10个历史数据的平均作为目前\(L_t\)情况的估计,进而带入公式来采样下一个t的选取
最终的训练变得很稳定,如上图的绿线
Improving Sampling Speed
这一部分提到了可以加速采样
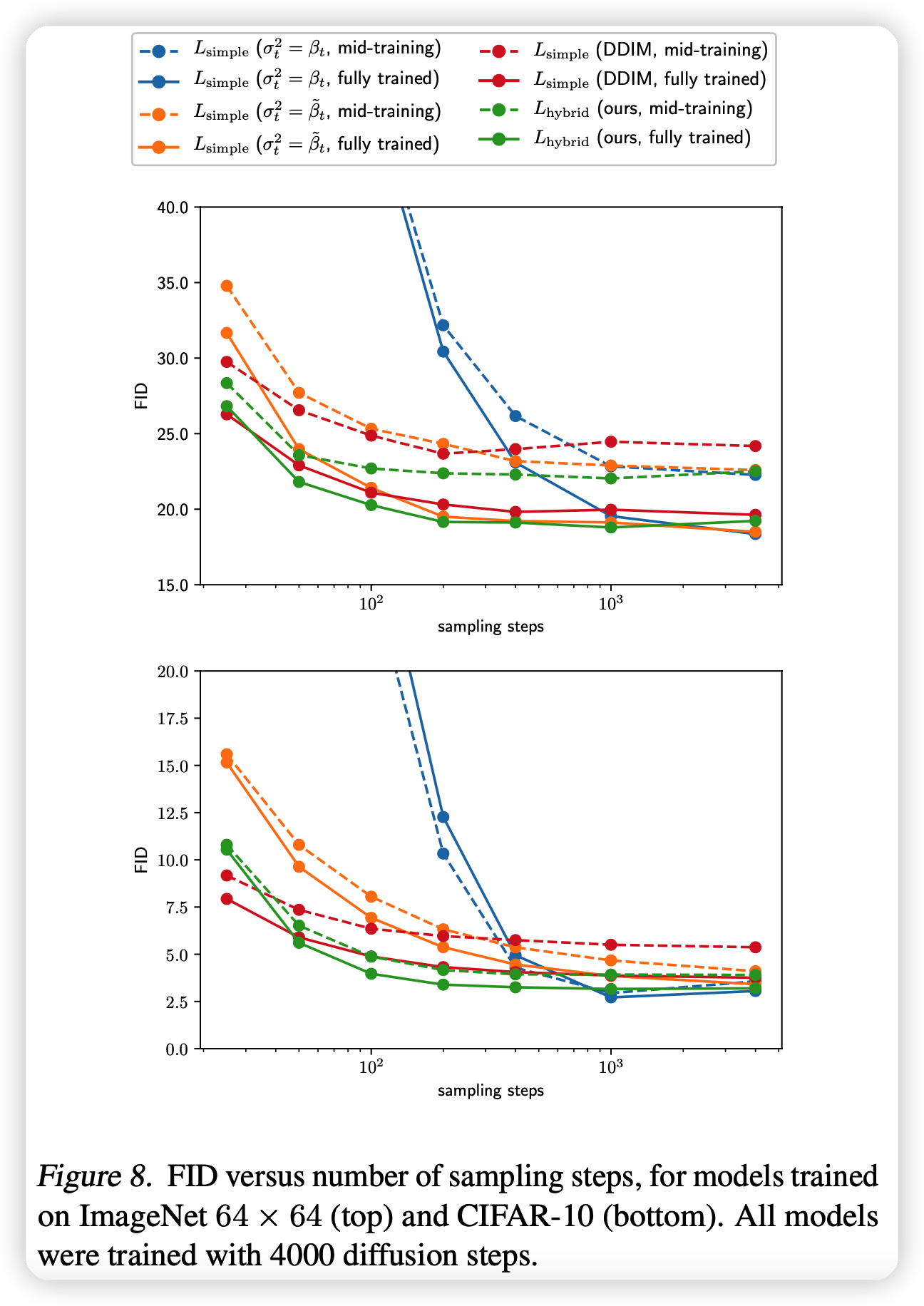
这里主要对比的是DDIM,方法也差不多:采样一个\(1,2,...T\)的长度为K子序列进行sample
可以发现,DDIM的没有IDDPM好:
- DDIM没有做IDDPM里这些改进。
- 作者提到没法做改进,这是因为DDIM的公式里的方差项没了
## Scaling Model Size
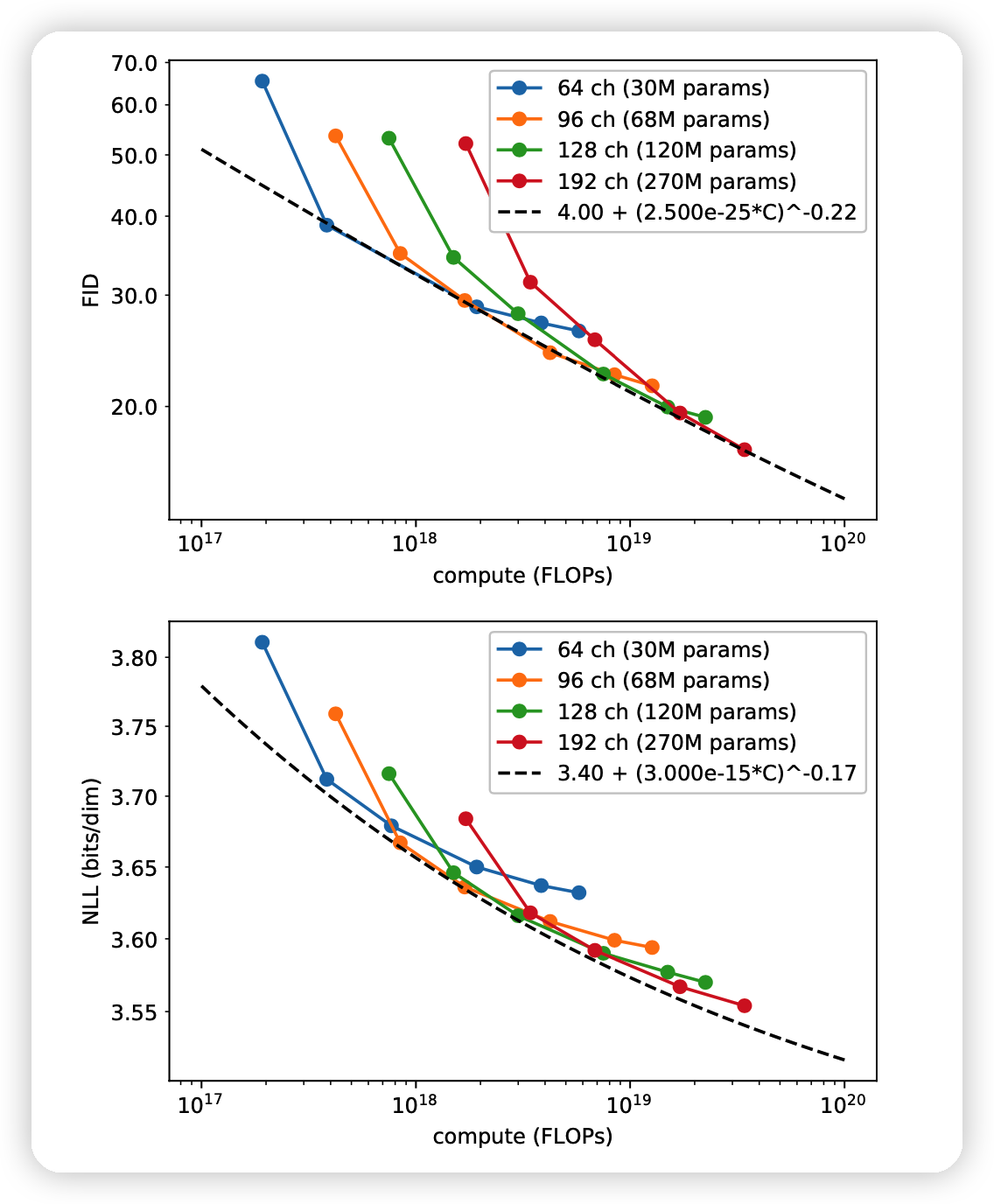
这一部分是分析DDPM模型在加大size以后会不会变得更好,因此作者直接加参数
- FID得分和模型的参数(计算量)基本呈线性关系。满足power law,因此扩大规模是个好选择
- NLL得分不满足线性关系,扩大规模效果不好,可能原因有:
- 很快过拟合
- loss不稳定
- 作者没有直接优化降低NLL用的\(L_{VLB}\),而是一个\(L_{\text{hybrid}}\)
我的思考
- 总体而言,这篇文章更像是分析性文章,复习笔记。主要方法还是DDPM。
- OpenAI研究员解决问题的眼光真的很高明呀,尤其是关于改变t选取和分析scale能力这一部分。