今天读了一篇编译,接下来回到老本行,来一篇diffusion model。这篇工作很有名,有点碰瓷DDPM的意思,其中“IMPLICIT”的意思是隐含。和DDPM的“probabilistic”相比,意思是减少随机性,加速采样。作者自己在AI Time上有个报告,好挺好的。
这篇工作和别的diffusion model工作一样,比较数学,很多推导我就不详细写了,可以从附录里看。
Introduction
大概意思就是:
- GAN很好,但今年的DDPM也不差
21年有一篇OpenAI的 BEAT GANS,用了DDIM,关注度很高,意思就是DDPM真的比GAN好
- DDPM的问题是慢
- 在CIFAR-10做32x32要20h
- 在CIFAR-10做256x256要1000h
- 本文解决这个问题,通过一个非马尔科夫的过程
Background
作者先讲了一般的DDPM是怎么搞的,这个叙述方式挺好的,讲讲重点
有一个公式: \[ q(x_{1:T} | x_0) := \prod_{t=1}^T q(x_t |x_{t-1}) \\ q(x_t |x_{t-1}) := N(\sqrt{\frac{\alpha_t}{\alpha_{t-1}} } x_{t-1},(1- \frac{\alpha_t}{\alpha_{t-1}})I) \] 也就是说,正常的DDPM是一个马尔科夫过程,想要从\(X_0\)得到后面,需要一步一步加噪声。这个噪声是一个高斯分布,其均值和\(X_{t-1}\)有关,是sample出来的。
反向的公式是: \[ q(x_{t−1}|x_t,x_0) = N(x_{t−1};μ_t(x_t,x_0),\hat{\beta_t} I), \] 其中 \[ \text{均值:} \mu_t(x_t,x_0) = \frac{ \sqrt{ \overline{\alpha_{t-1}} }\beta_t }{1 - \overline{\alpha_{t}}} x_0 + \frac{\sqrt{\alpha_t} (1 - \overline{\alpha_{t-1}} )}{1 - \overline{\alpha_{t}}} x_t \\ \text{方差:} \hat{\beta_t} = \frac{1 - \overline{\alpha_{t-1}}}{1 - \overline{\alpha_{t}}}\beta_t \]
另一方面,由于这个高斯分布的传递性,我们可以把\(x_t\)视为单位高斯分布和\(x_0\)的线性叠加: \[ x_t = \sqrt{\hat\alpha_t} x_0 + \sqrt{1 - \hat\alpha_t} \epsilon, \quad \epsilon \sim N(0,I) \] 我们在训练时我们想要让 \(\log p_\theta(x_0) \to \log q(x_0)\),也就是说,我们想要优化: \[ L_{t-1} = E_q [ \frac{1}{2\sigma^2} || \mu_t(x_t,x_0) - \mu_\theta(x_t,t)||^2] \] 其中
左边是实际马尔科夫链对\(x_{t-1}\)的估计,可计算
右边是我们的去噪模型\(\theta\)对\(x_{t-1}\)的估计,可计算
这里我们套入上面\(x_t\)的公式,看做\(x_t,\epsilon\)的函数,进行一波化简,最终得到 \[ L_{t-1} = C * \frac{1}{2\sigma^2} || \epsilon - \mu_\theta(\sqrt{\hat\alpha_t} x_0 + \sqrt{1 - \hat\alpha_t},t)||^2 \] 忽略常数C,同时对所有的L进行优化: \[ L_{\text{simple}} = \sum_{t=1}^T L_t \] 就能学出DDPM模型了
VARIATIONAL INFERENCE FOR NON-MARKOVIAN FORWARD PROCESSES

上面全是DDPM的数学推导。接下来,作者讲了他的贡献。它发现:
- DDPM中的loss\(L_\lambda\)只依赖于\(q(x_t|x_0)\),和\(q(x_{1:T} |x_0)\)无关。这样符合边缘分布的可能性有很多,作者选取了一个非马尔科夫的过程
\[ q_\sigma(x_{1:T} |x_0) := q(x_{T} |x_0) \prod_{t=2}^T q_\sigma (x_{t−1} |x_t , x_0 ) \\ q_\sigma (x_{t−1} |x_t , x_0 ) = N \left( \sqrt{\alpha_{t-1}}x_0 + \sqrt{1 - \alpha_{t-1} - \sigma^2_t} \times \frac{x_t - \sqrt{\alpha_t}x_0}{\sqrt{1-\alpha_t}} , \sigma_t^2 I\right) \]
接下来,对于 \(x_0 \sim q(x_0) , \epsilon_t \sim N (0, I)\)我们可以获取其对应的\(X_t\),由 \[ x_t = \sqrt{\hat\alpha_t} x_0 + \sqrt{1 - \hat\alpha_t} \epsilon_t \] 如果我们有一个对\(\epsilon_t\)的预测器\(\epsilon_\theta^{(t)}(x_t)\)输入不含\(X_0\)。我们可以用他来预测\(X_0\): \[ f^{(t)}(x_t) := (x_t − \sqrt{1 − \alpha_t} · \epsilon^{(t)}(x_t))/\sqrt{\alpha_t} \] 由此,这个去噪的过程可以看做: \[ p_\theta^{(t)}(x_{t-1} | x_t) = q_\sigma (x_{t−1} |x_t , f^{(t)}(x_t) ) \] 式子右边只和\(x_t,\epsilon\)有关
作者接下来证明了这个算法的train过程用到的loss和DDPM是等价的(差一个常数)。也就是说,训好的DDPM模型可以认为是训好的DDIM模型
sample
这个模型是怎么infer的呢?
进一步展开、化简刚才的\(p_\theta^{(t)}(x_{t-1} | x_t)\),我们可以得到
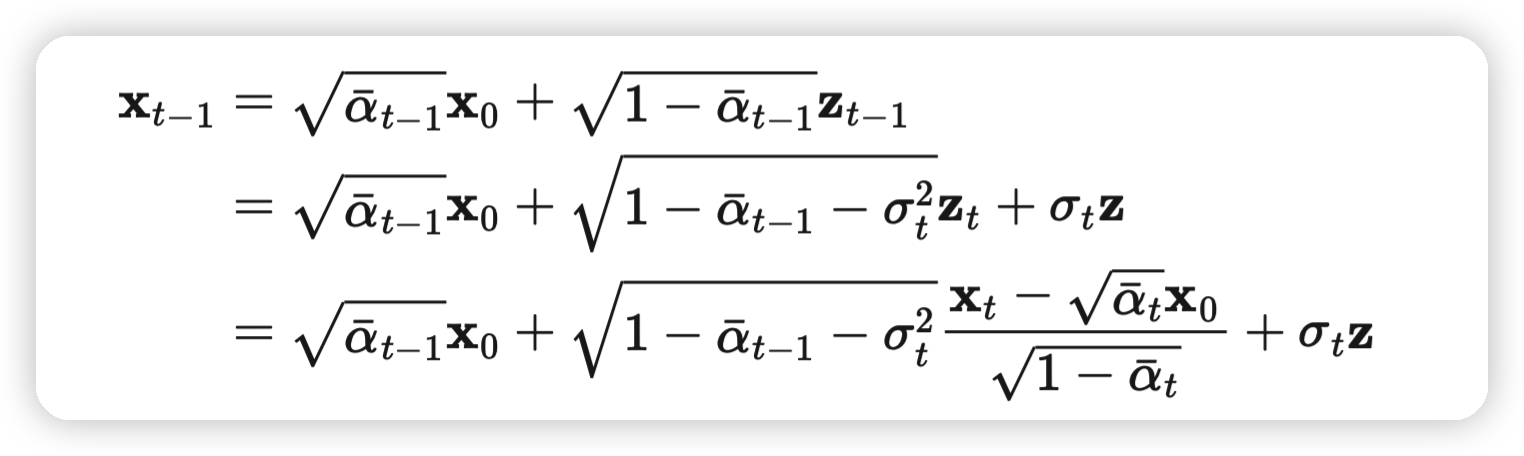
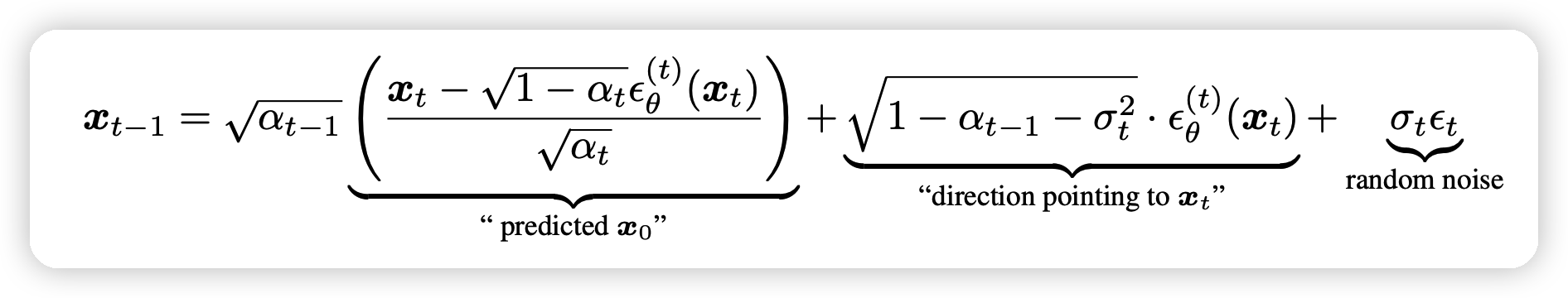
这个式子里面只有最右边的部分是带有随机成分的。而且当 \[ \sigma_t = \sqrt{(1 − \alpha_{t−1})/(1 − \alpha_{t})}\sqrt{1 − \alpha_{t}/\alpha_{t-1}} \] 时退化为DDPM
如果我们取\(\sigma_t = 0\)。式子有确定性的输出,这个模型称作DDIM。
ACCELERATED GENERATION PROCESSES
说完了采样,那么加速在哪呢?
作者证明了:
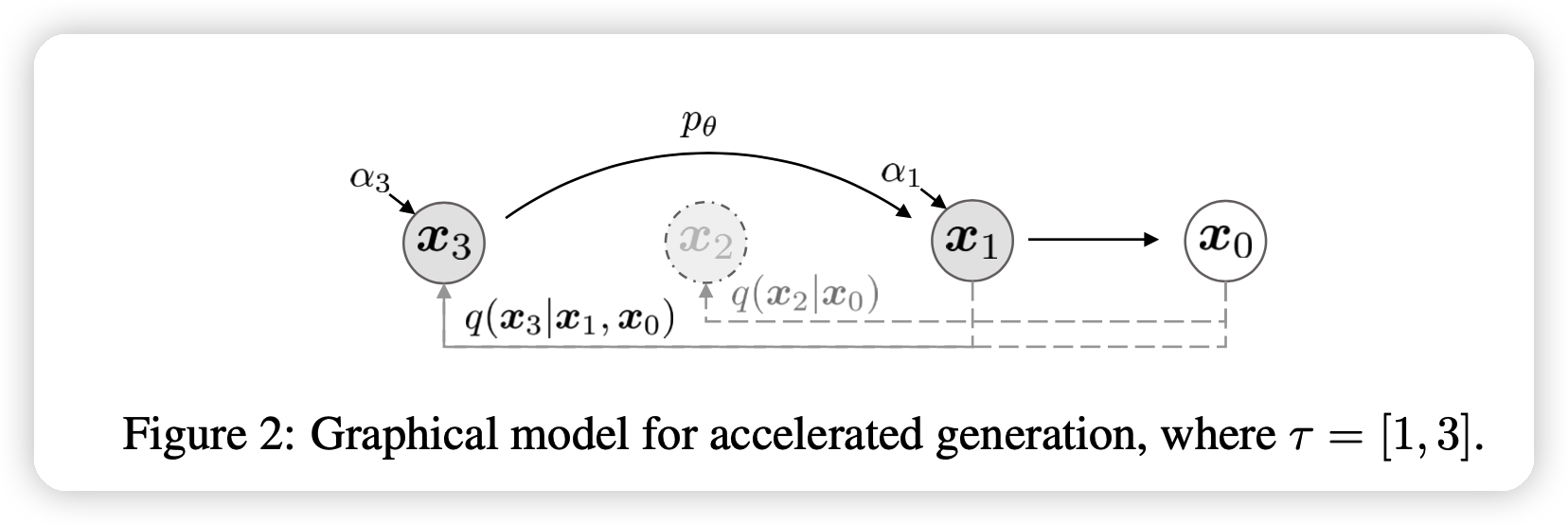
- 上面的逆过程不需要从\(T,T-1,...,1,0\)一路下降,其实选取一个递减的子集也是可以的!
实验
实验部分,作者实际上选取了: \[ \sigma_t = \eta \sqrt{(1 − \alpha_{t−1})/(1 − \alpha_{t})}\sqrt{1 − \alpha_{t}/\alpha_{t-1}} \] 其中\(\eta\)是超参,0代表是DDIM,1代表是DDPM。另一个变量是选取的子集S的大小(\(|S|=1000\)代表没有简化),跑了这个图:

可以看出,DDIM在步数少的时候表现最好。最下面那个\(\hat\sigma\)代表原始的DDPM祖先采样。可以看出,衰减非常明显
作者还提到了这个方法的另一个优势:
- 由于确定性的增加,相同的初始噪声映射到基本相同的结果。可以方便做图片的修改。

我的思考
- 虽然证明和数学过程很复杂,但结论却是惊人的简单:同样的DDPM,换一个采样方法,就能加速50倍
- 这个感觉是对上面论文ODE的一种实现?作者在论文里也用一小节说了这事。
- 有个后文 DPM-Solver,10步就能媲美DDPM-1000步,过两天笔记整上