这篇论文是朱军老师组做的工作,非常的数学。
Introduction
- DPM生成很慢,这是因为逆过程对方差的估计花了额外的时间
- 本文发现最优的期望和方差竟有解析形式(iDDPM岂不是优化了个寂寞…)
- 本文用蒙特卡洛模拟最优方差,预计算
- 在获得更高质量图片的同时得到了80倍的速度提升(对,效果甚至更好)
- 本文在选取快速路径时用动态规划
- 本文是plug-and-play的,任何DPM模型拿过来换个\(\sigma\)就行
Background
重新说了一下DDIM里的推广形式:
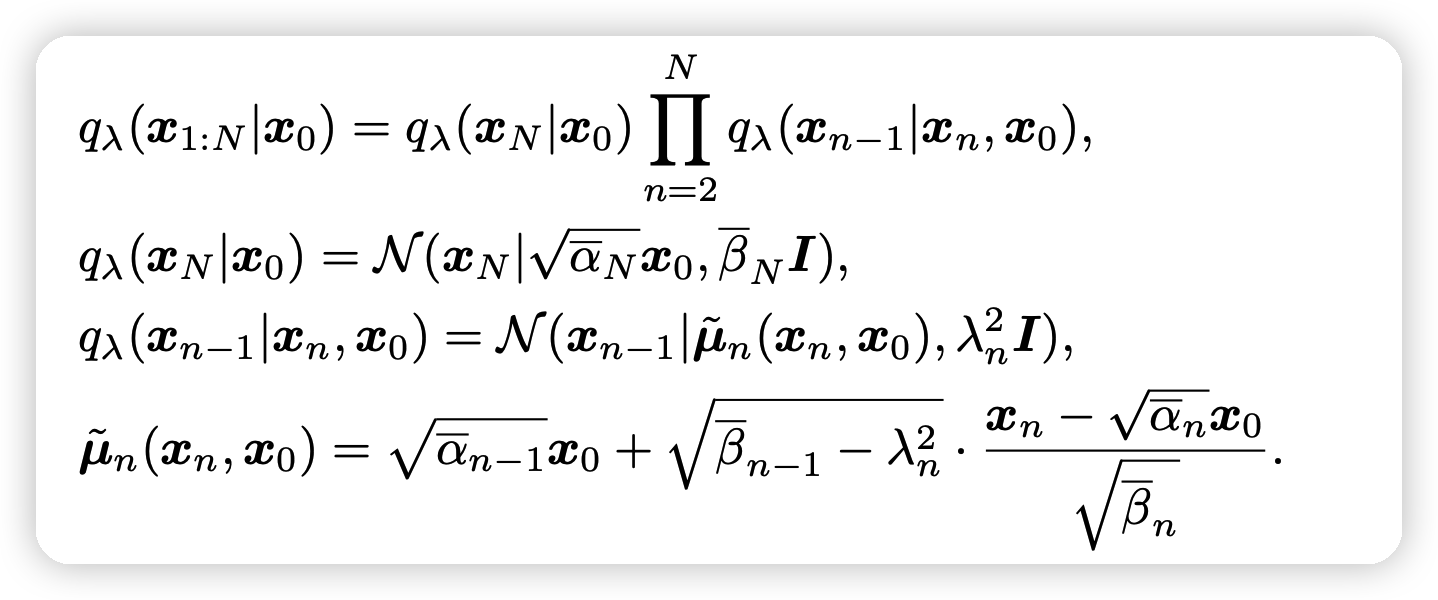
其中\(\overline{\alpha}:=\prod_{i=1}^N \alpha_i, \overline{\beta} := 1-\overline{\alpha}\)
- 当\(\lambda_n^2 = \tilde{\beta_n} := \frac{\overline{\beta}_{n}}{\overline{\beta}_{n-1}}\beta_n\)时,模型就会推导出DDPM
- 当\(\lambda_n^2 \equiv 0\)时,就是DDIM
上面这种前项过程的逆过程是一个马尔科夫过程: \[ p(x_{0:N}) = p(x_N) \prod_{n=1}^N p(x_{n-1}|x_n), \quad p(x_N) \sim \mathcal{N}(0,I) \\ p(x_{n-1}|x_n) = \mathcal{N}(x_{n-1}| \mu_n(x_n),\sigma_n^2 I) \] 其中\(\mu_n(x_n)\)用一个score based model来学习\(s_n(x_n)\), \[ \mu_n(x_n) = \tilde{\mu}_n\left( x_n,\frac{1}{\sqrt{\overline{\alpha_n}}} (x_n +\overline{\beta_n} s_n(x_n) ) \right) \] 如果认为\(s_n(x_n) = -\frac{1}{\sqrt{\overline{\beta_n}}} \epsilon_n(x_n)\),这和DDPM的推导结果是一致的
对于方差的估计:
- DDPM使用\(\sigma_n^2 = \beta_n或\sigma_n^2 = \tilde{\beta}_n\)
- DDIM使用\(\sigma_n^2 = \lambda_n^2\)
作者说,这实际上是一个负优化
ANALYTIC ESTIMATE OF THE OPTIMAL REVERSE VARIANCE
接下来引入文章的本体,作者证明了上述定义的DPM的逆过程的均值、方差的最优形式:

这个结论的证明非常复杂,感兴趣的同学可以看附录A
只要按照上面的式子进行去噪,就能得到最好的结果,到达模型的极限能力
对应的SDE的连续时间形式,也有类似的结论,参考附录(目前用不上)
可以看出,上面的均值部分和已有方法的优化的\(\mathcal{L}_{LVB}\)具有一样的形式,因此现在的DDPM等模型的训练就是在逼近最优的均值,训练没有问题。
接下来,作者就要把之前的手动设计的方差替换为解析的形式,对于后面的密度项,作者使用蒙特卡洛进行估计 \[ \Gamma_n = \frac{1}{M}\sum_{m=1}^{M} \frac{ || s_n(x_{n,m})||^2 } {d} , \quad s_{n,m}\mathop{\sim}^{i.i.d} q_n{x_n} \]
\[ \hat{\sigma}^2_n = \lambda_n^2 + \left( \sqrt{\frac{\overline{\beta_n}}{\alpha_n}} - \sqrt{\overline{\beta}_{n-1} - \lambda_n^2 } \right)^2 (1 - \overline{\beta}_{n}\Gamma_n) \]
- 这个方差和训练无关。在模型训练以后,可以预计算出来每一步的方差,再统一的进行infer
- 随着蒙特卡洛采样数M的增大,这个估计会越来越准确,逐渐逼近最优的方差。作者提到,取M=10,100基本上就收敛了
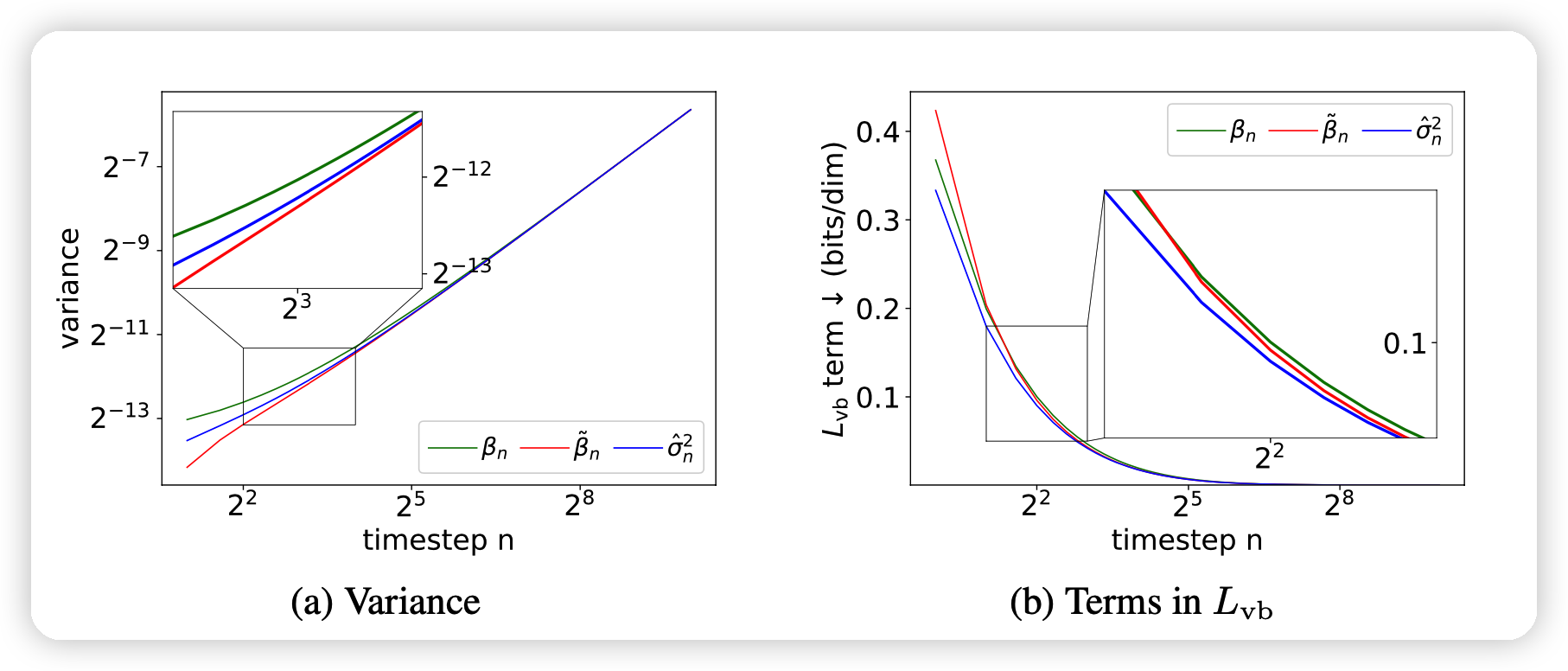
下面这个图
- 显示出了作者的估计值和DDIM和DDPM手动设计的方差的区别
- 显示了作者的方差对于\(L_{vb}\)是最小的,这个应该是针对一次infer而言。
BOUNDING THE OPTIMAL REVERSE VARIANCE TO REDUCE BIAS
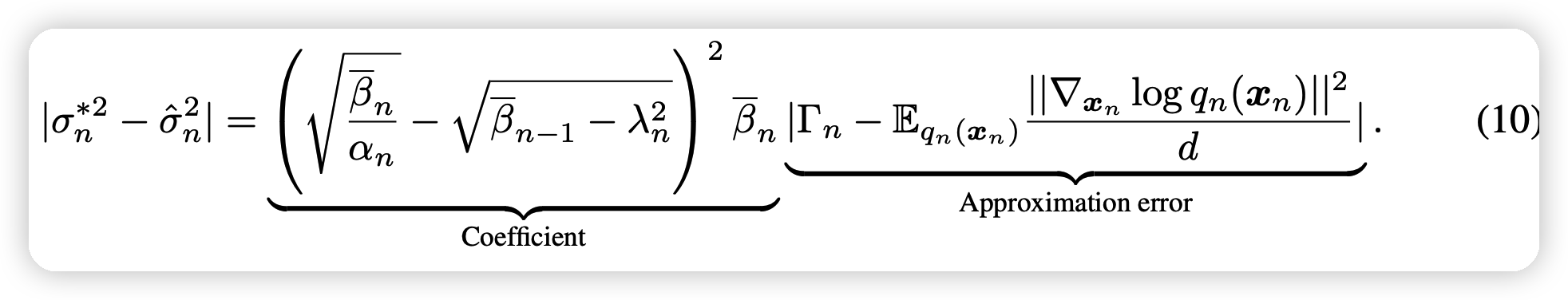
这一部分,作者分析了他的逼近形式和真正的最优形式之间的bias:
- 由于模型的训练,会带来不可避免的误差(因为不可能有完全没误差的模型)
- 如果在sample时选取一个较短的路径,左边的coefficient部分会变大
接下来,作者尝试能不能减小误差,作者又证明了真实方差的上下界

- 这个上下界都是确定的、和模型训练无关的,在选定了\(\beta_n\)之后就唯一确定了。
- 同时作者证明了(12)中的上界是一个比较接近真实值的上界。
因此,作者才计算完拟合的方差\(\hat{\sigma}_n\)之后可以用上下界再做一次CLIP。
ANALYTIC ESTIMATION OF THE OPTIMAL TRAJECTORY
这一部分,作者讲了在一个缩减的去噪路径中优化的方法。还是先提到了DDIM优化的故事线:
- 其中 $1 = _1 < _2 ... < _K = N $,把一个长为N的路径变成了长为K的采样路径
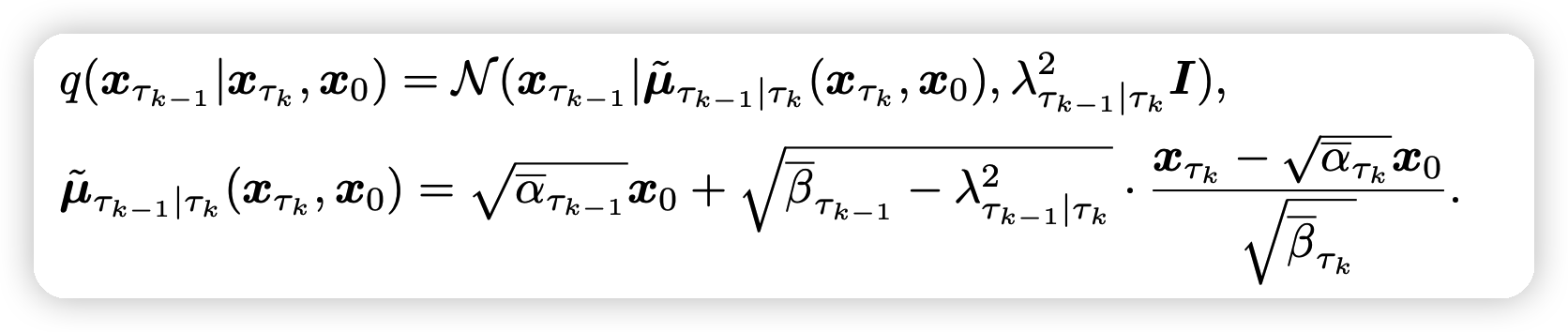
在这个过程中,我们的\(\lambda^2_{\tau_{k-1}| \tau_k}\)也可以变成拟合的新形式:
- 其中的\(\Gamma_{\tau_{k}}\)可以在\(\tau_{k-1} \sim \tau_{k}\)之间通用
\[ \hat{\sigma}^2_{\tau_{k-1}| \tau_k} = \lambda_{\tau_{k-1}| \tau_k}^2 + \left( \sqrt{\frac{\overline{\beta_{\tau_k}}}{\alpha_{\tau_{k-1}| \tau_k}}} - \sqrt{\overline{\beta}_{\tau_{k-1}} - \lambda_{\tau_{k-1}| \tau_k}^2 } \right)^2 (1 - \overline{\beta}_{\tau_{k-1}}\Gamma_{\tau_{k}}) \]
上面的推广是显然的,然而,路径的选取大有说法,
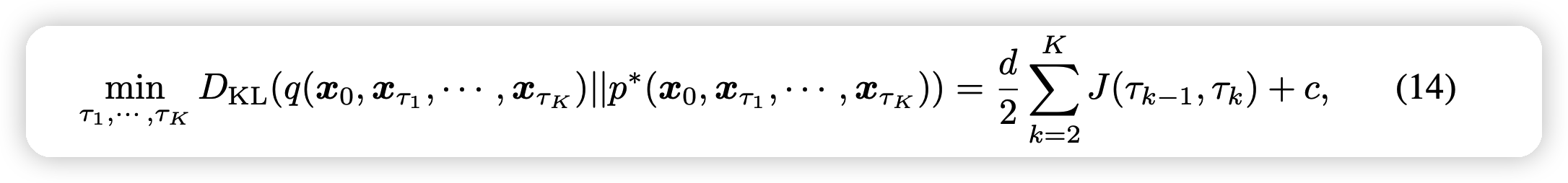
作者竟然推导出了一个K路径中模拟的偏差的下界:
- 其中\(J(\tau_{k-1},\tau_k) = \log (\frac{\sigma^{*2}_{\tau_{k-1}| \tau_k}}{\lambda_{\tau_{k-1}| \tau_k}^2})\),c是一个和路径选择无关的量
- 如果把\(\sigma^{*} \sim \hat{\sigma}\)的话,这个最小值就是可计算的,只要路径被选定
甚至,这是一个动态规划问题,从T里选取K个数,要求K个数的损失之和最小,每个数的损失都是确定的。在模型训练完、K被选定后,可以执行一次算法,得出具体怎么选会得到最小的损失

RELATIONSHIP BETWEEN THE SCORE FUNCTION AND THE DATA COVARIANCE MATRIX
这一部分是说了score function和协方差矩阵之间的关系。今天作者在ICML的另一篇论文推广了这个优化,这篇就不讲了。
Experiment
这里作者用了:
自己在CIFAR-10上分别用cosine和linear两种\(\beta\)炼出来的CIFAR-10(LS), CIFAR-10(CS)
DDPM和DDIM在ImageNet上预训练的开源模型,分别使用和不使用Analytic方差
作者在全部模型上CLIP了方差,因为这个上下界是恒存在的

这个结论是很明显的,可以说是吊打:
- 凡是加上了拟合方差的,基本上都比不加要好
- 对于K小的时候,会很明显
- 当T=K的时候,总的效果也要更好
- 甚至用了50步,就战胜了普通DDIM 1000步的效果
当然作者也提到了几个现象:
- Analytic的形式不是永远比不用要好,这和解析形式的“最优”结论是不一致的
- K更大时效果不一定会更好
- 用动态规划OT的K选取不一定总是最好的
我的想法
- DDPM里面有一点就是,去噪方差要手动设置。
- 一个直观的想法就是,如果方差里也引入模型,效果会更好。iDDPM就是用模型来学习方差,但收敛难(参考GAN)
- 这篇文章结论就是:用学均值的模型,可以顺便用一个蒙特卡洛模拟来近似最优的方差!不需要额外学!
- 这篇文章正文没有一个图片,就拿了ICLR outstanding paper,值得唏嘘。正文10页,附录29页,基本全是数学证明,可见AI的本质是数学(
- 作者在附录中的future work里说后面要做speech领域,用上面说的最优形式的连续时间推广形式。我们是不是想办法看看NLP怎么用