这篇讲了一种借鉴Discrete Diffusion model来建模一个order-agnostic autoregressive模型的方法,在text8数据集取得不错的效果。

这篇论文发表在ICLR22上,作者来自google brain。
background
首先梳理几个概念
ARM
自回归数据集里的每句话: \[ \log p(x) = \sum_{t=1}^D \log p(x_t | x_{<t}) \] 用一个上三角矩阵把每句话mask住做D次predict就能算出模型对本次数据的loss
Order Agnostic ARMs
XLNet采用这个结构,就是说模型不是从左到右预测的,而是按照任何一个顺序都可以: \[ \begin{aligned} \log p(x) & = \log \mathbb{E}_{\sigma \sim \mathcal{U}(S_D)} \sum_{t=1}^D p(x_{\sigma(t)} | x_{\sigma(<t)})\\ & \geq \mathbb{E}_{\sigma \sim \mathcal{U}(S_D)} \sum_{t=1}^D \log p(x_{\sigma(t)} | x_{\sigma(<t)}) \end{aligned} \] 这个公式里,\(\sigma\)是对\(1,2,...D\)的一个重排。大概就是给定一个重排,按照这个重排的前一部分信息,生成剩下的每一个位置\(\sigma(t)\)的量。
式子中的不等式来自杰森不等式
从左到右可以看做一种特定的重排。上面式子相当于对所有重排的总的loss的期望,训练时任选一个重排就行
Discrete Diffusion
这里引用的是21年的论文,大概就是把MLM视为某种diffusion model,是文本领域diffusion model的一种解法
AUTOREGRESSIVE DIFFUSION MODELS
method
这一部分讲本文的方法
上来就是loss的公式计算,作者用了不同的推导方式: \[ \begin{aligned} \log p(x) & \geq \mathbb{E}_{\sigma \sim \mathcal{U}(S_D)} \sum_{t=1}^D \log p(x_{\sigma(t)} | x_{\sigma(<t)}) \\ & = \mathbb{E}_{\sigma \sim \mathcal{U}(S_D)} D \times \mathbb{E}_{t \sim \mathcal{U}(1,2,..D)} \log p(x_{\sigma(t)} | x_{\sigma(<t)}) \\ & = D \times \mathbb{E}_{t \sim \mathcal{U}(1,2,..D)} \mathbb{E}_{\sigma \sim \mathcal{U}(S_D)} \frac{1}{D-t+1} \sum_{k\in \sigma(> t)} \log p(x_{k} | x_{\sigma(<t)}) \end{aligned} \] 这个公式有几个特点:
- 他进一步考虑了XLNet中没有考虑的时间t
- 他把”重排中剩下位置“当成了”很多个原子的生成过程的并行“的形式
具体而言他定义了:
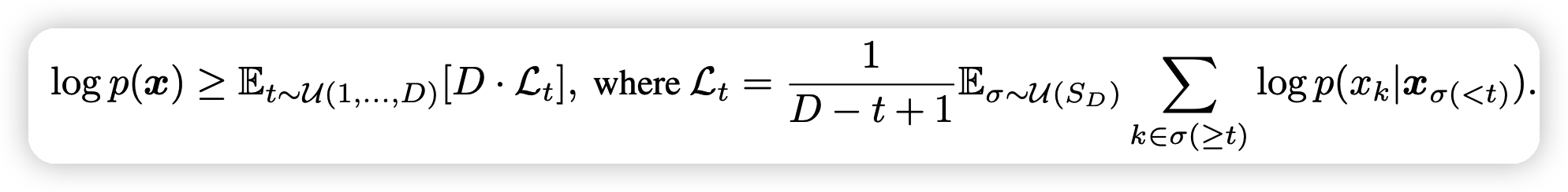
上面的式子就比较好理解了:\(\mathcal{L}_t\)的计算只和\(t,\sigma\)有关,可以视为把句子mask住一些位置,然后预测剩下的每一个位置的loss之和(BERT loss之和),再加上一个正则量
具体训练中,作者直接使用transformer结构,然后就直接用下面的算法进行训练和预测:

其中:
- m是一个布尔向量,代表重排\(\sigma\)的前t-1个位置是1
- m是一个布尔向量,代表重排\(\sigma\)的第t个位置是1
- \(\bigodot\)是指和布尔向量乘,布尔0位置置为0
- \(\mathcal{C}\)是一个cat分布,代表以\(f(m\bigodot n)\)的概率分别取K(词表大小)个值中的一个
对于NLP而言,可以直接设定一个词表K外的词K+1代表MASK,word embedding为a,然后就能在代码上比较统一: \[ \text{mask}(x,m) = m \bigodot x + (1-m)\bigodot a \]
PARALLELIZED ARDMS
这一部分,作者分析了上面公式中的并行性的特点带来更快的解码速度。因为如果有t个位置的结果以后,解码剩下的位置都是并行的,
如果假设\(L_{t,t+k} = \sum_{i=1}^k\mathcal{L}_{t+i} \approx k \mathcal{L}_t\),视为解码所需要的代价
那么用一个动态规划算法,就能算出使得代价最小的并行化解码方法(固定解码步骤\(c\))。下图就是把一个20步的解码只用5步来完成
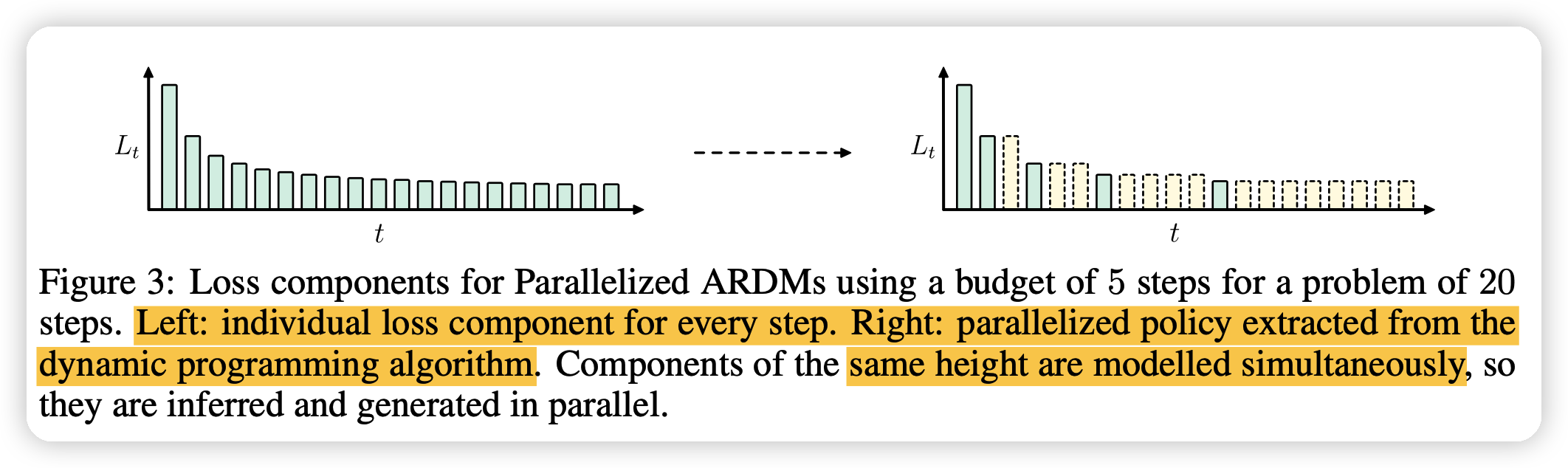
Experiment
这一部分作者,用bpc的NLL loss来对比了作者的方法OA-ARDM,和之前的离散diffusion方法\(D3PM-*\),所有模型用的结构是一样的,只有训练方法和采样方法不一样

- 可以看到主试验的结果基本完胜 Austin 21的方法。
- 值得一题的是,效果没有从左到右的auto-regressive好(一个普通transformer baseline结果是1.35)
- 另一方面就是新的结果由于比较好的并行性,只用20步的解码就可以达到之前大概250步的结果
- 实验用的数据集是text8,解码的例子如下:
