这一篇文章可以看做对Intrinsic Dimension的又一个推广,用了比LoRA更强的假设。通过在多任务间找到统一的子空间表示,证明了任务间的相关性,提升了prompt tuning的稳定性和效果

作者是THUNLP实验室
介绍
这篇文章主要是探讨这个问题:
已有研究发现预训练可以降低下游任务的Intrinsic Dimension,也就是模型可以压缩下游任务的表征
那么不同的下游任务需要的空间是否是关联或者统一的呢?
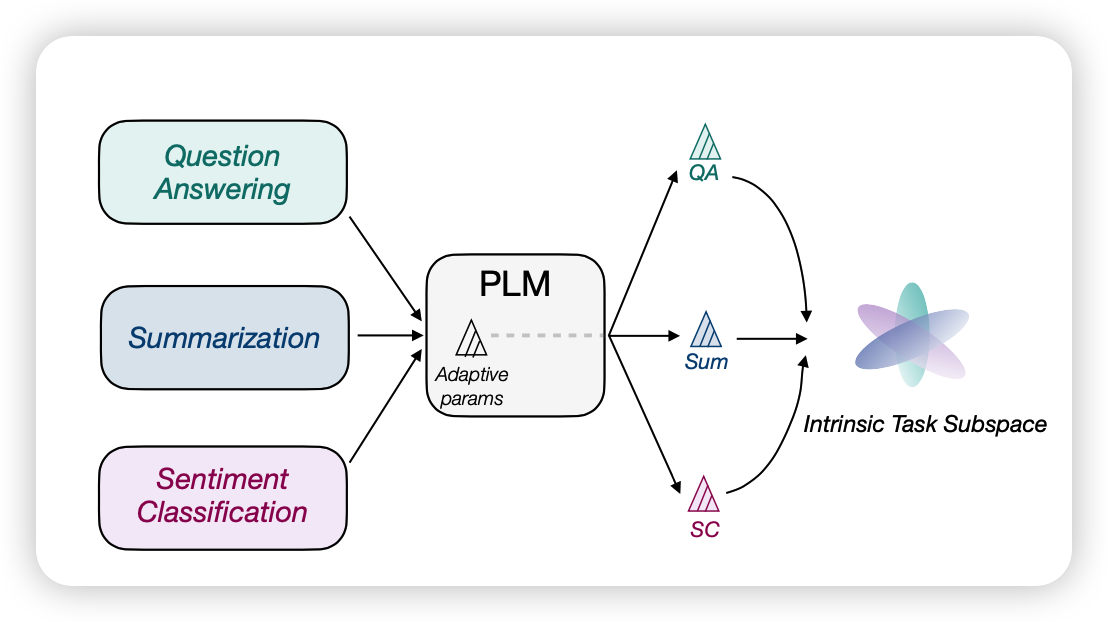
由此作者进行了一系列的探索,发现竟然可以只用250个参数统一子空间上就能在100个可见任务和250个不可见任务上达到FT的97%和83%的效果
全文的实验设计很复杂,对比也很多,我感觉文章的组织形式和结论更像是一种探索、分析性的文章
方法
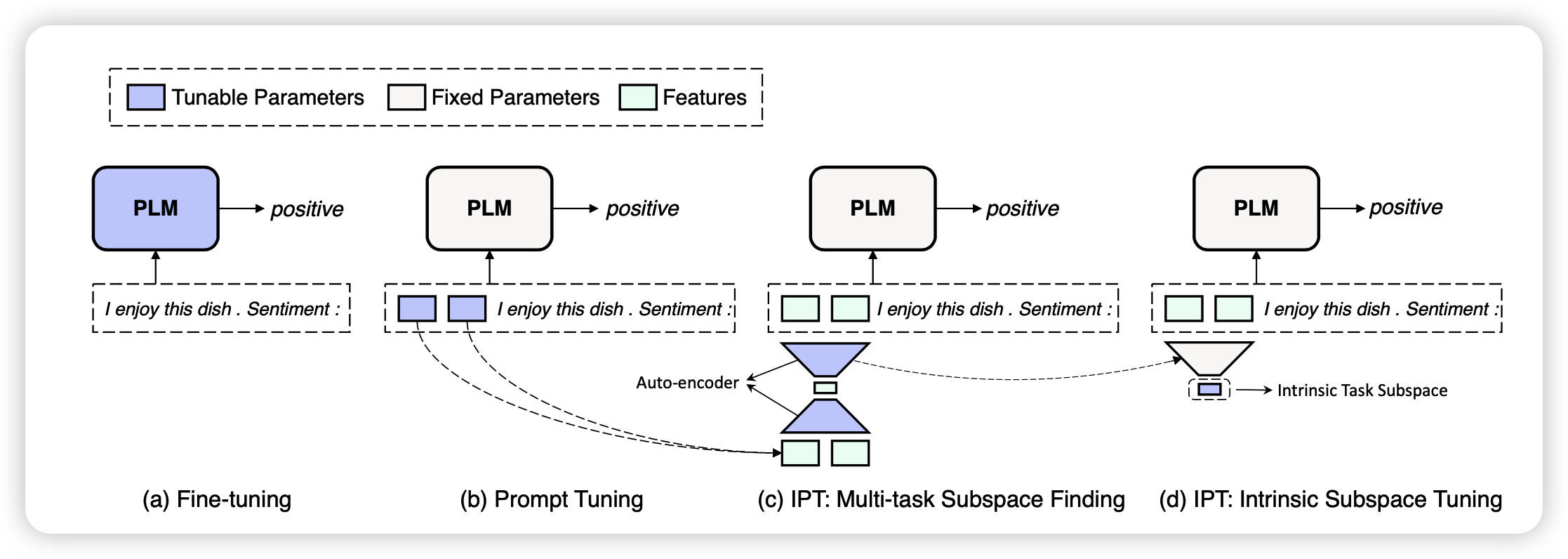
具体怎么实现统一的子空间呢?作者分为了两个步骤:
- Multi-task Subspace Finding (MSF)
- Intrinsic Subspace Tuning (IST)
Multi-task Subspace Finding (MSF)
这个过程实际上就是在寻找任务统一的子空间,首先要确定“任务”是什么意思:
对于一个任务而言,就是一个\(<X,Y>\)的集合,其中X是输入语句,Y是一个类别(分类任务)或者一些句子(生成任务)。
所谓的PT就是在任务输入X前面加上一个可学习的prompt,实际模型是这样的: \[ \mathcal{L}_{PT} = -\frac{1}{|\mathcal{Y}|} \prod_{j=1}^{|\mathcal{Y}|} P(y_j | p_1,p_2,...,p_n,x_1,x_2,...,x_{|\mathcal{X}|}, y_1,...,y_{j-1}) \] 保持只有\(p_1,...,p_n\)是可学习的,别的参数都锁定,然后参数p是从某个分布采样来进行初始化的
作者首先找到了120个已有任务,把他们随机分成了100个可见任务和20个不可见任务
由此可见,PT正常的搜索空间是\(D = n\times d(\text{model dimension})\)的,对于不同的任务,模型可以加上不同的prompt来进行表示。对于100个任务,一共有100组prompt(在每个任务的训练集上训练得来的)
那么怎么找到统一的表示空间呢?
可以先把D维降到d维,再来一个反向变换变换回D维。如果锁定矩阵的话,中间的d维就是所谓的统一表示空间,矩阵就是空间的变换矩阵。在具体执行中,使用重建loss进行学习: \[ \begin{aligned} P_i^* & = \text{Proj}_b(\text{Proj}(P_i)) \\ \mathcal{L}^i_{AE} & = || P_i^* - P_i ||^2_2 \\ \mathcal{L}^{MSF}_{\theta_{proj}} & = \frac{1}{|\mathcal{T}_{train}|} \sum_{i=1}^{|\mathcal{T}_{train}|} (\mathcal{L}_{PT}(P_i^*) + \alpha \mathcal{L}^i_{AE}) \end{aligned} \] 通过这公式,可以学习到前后的变换模型的参数。实验中,变换模型就是简单的MLP
Intrinsic Subspace Tuning (IST)
一旦学习好变换矩阵\(Proj,Proj_b\)以后,对于新的任务,我们就可以只保留\(Proj_b\)矩阵,然后从统一的子空间采样prompt \[ \mathcal{L}^{IST}_{\theta_{d}} = \mathcal{L}_{PT} (\text{Proj}_b(V_i)) \] 其中,只有d维变量\(V_i \in \mathbb{R}^d\)是可学习的
实验
这一部分作者做了各种实验来佐证文章的观点
作者找到了120个任务,随机分成100个可见任务和20个不可见任务;也可以按是否生成任务来分
可见任务是指训练proj时用到的prompt的任务
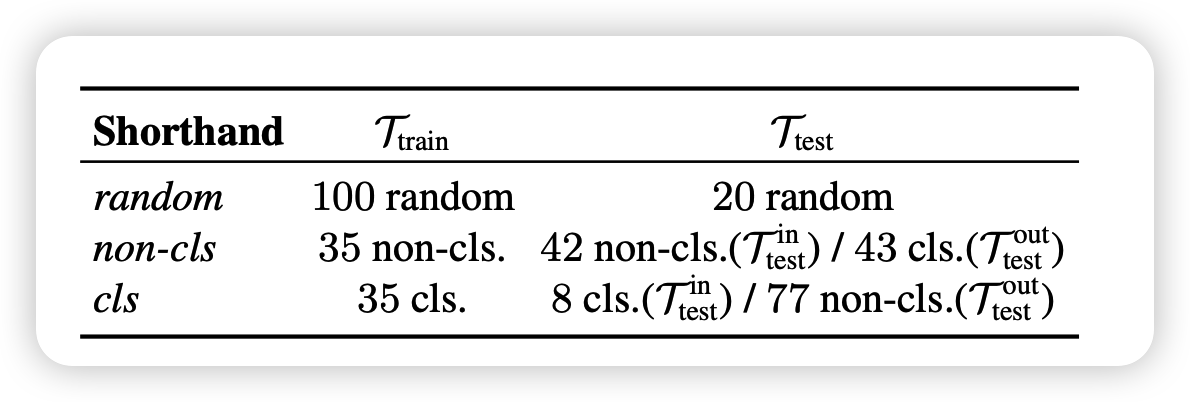
首先所有实验是用BART执行,然后所有任务都报告了相比于直接prompt tuning/fine tuning的结果的相对值,分类任务用F1,生成任务用BLEU。
所有任务都是few-shot场景下的:
- 生成任务用32条数据
- 分类任务用16条数据
其中模型用到的指标的解释如下:
- \(\mathcal{T}_{\text{train}}(\text{MSF})\): 在100个任务上训完\(Proj,Proj_b\),然后直接报告重建的prompt的表现
- \(\mathcal{T}_{\text{test}}(\text{MSF})\): 在20个不可见的任务上直接报告重建的prompt的表现(用不可见任务的训练集先做PT训练,把出来的prompt跑一遍重建)
- \(\mathcal{T}^{\text{same}}_{\text{train}}(\text{IST})\):拿训好的\(Proj_b\),在可见任务上从零开始做d维的 IST PT
- \(\mathcal{T}^{\text{diff}}_{\text{train}}(\text{IST})\):unseen-data challenge,对于可见任务在保持测试集不变的情况下,换用另外的训练集(和之前训正常prompt不一样的训练集)做IST PT
- \(\mathcal{T}_{\text{test}}(\text{IST})\):在20个不可见任务上做 IST PT
- \(\mathcal{T}^{in}_{\text{test}}(\text{MSF}),\mathcal{T}^{out}_{\text{test}}(\text{MSF})\):如果用是否用CLS划分任务的话,测试loss分为两组(就是生成和非生成任务)
实验结果如下:
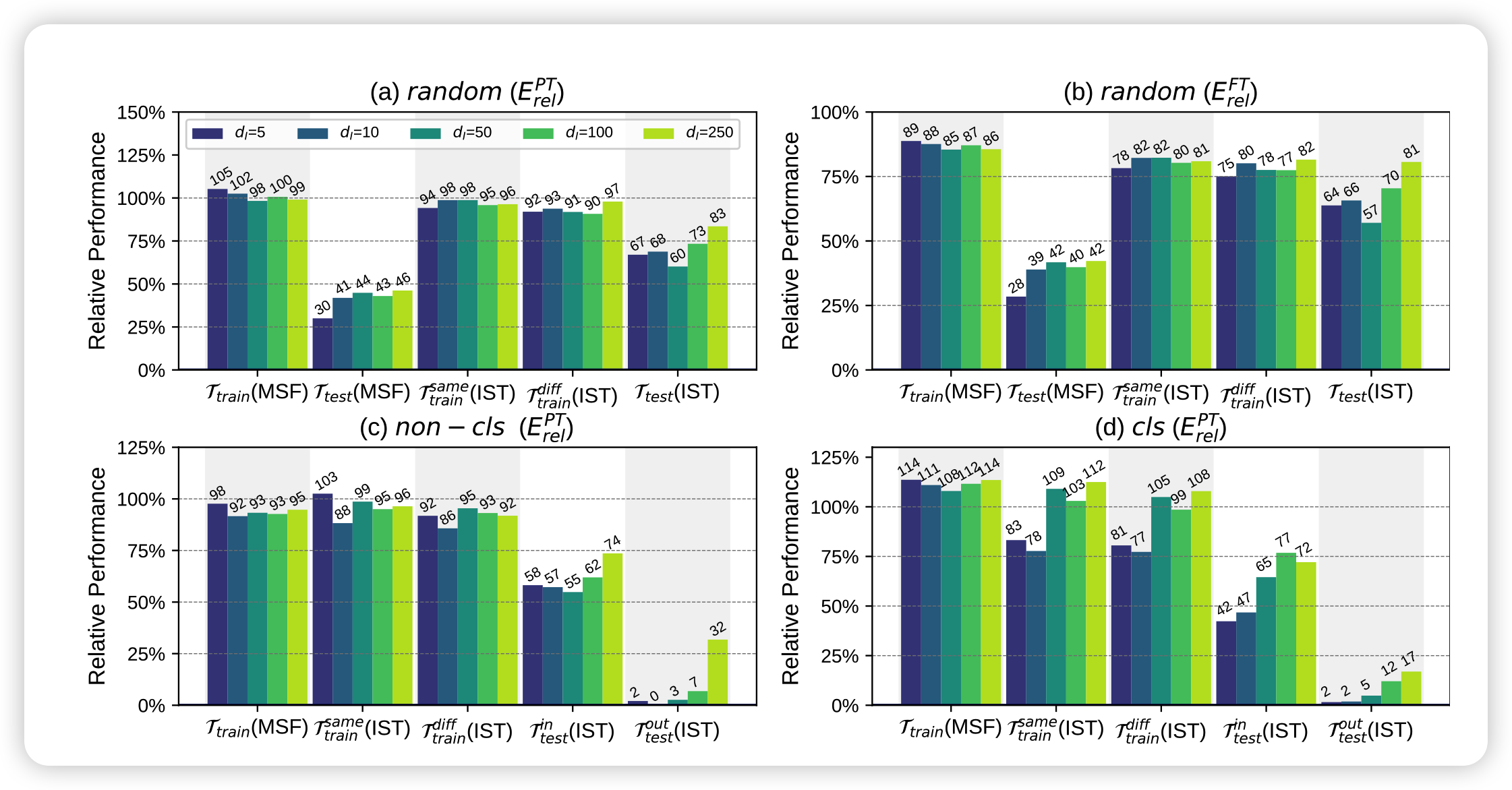
这个结果其实能说明很多问题,作者用了两页来讲这个结果,大致有以下几个关键点:
Do PLMs really reparameterize various task adaptations into a universal task subspace?
首先就是主试验的结果,发现\(\mathcal{T}^{\text{diff}}_{\text{train}}(\text{IST})\)和\(\mathcal{T}_{\text{test}}(\text{IST})\)效果都很好,这说明用一个统一的subspace确实可以得到很不错的效果,有力佐证了共同子空间假说
What limits IPT?
作者进一步分析IPT效果的提升空间
- \(\mathcal{T}_{\text{train}}(\text{MSF})\)和\(\mathcal{T}_{\text{test}}(\text{MSF})\)之间的差距不小,说明模型对于不可见任务的泛化能力弱小,这可能和变换模型的结构有关系
- \(\mathcal{T}_{\text{train}}(\text{MSF})\)和\(\mathcal{T}^{\text{same}}_{\text{train}}(\text{IST})\)的差距,说明模型从统一子空间学习的能力没有在高位空间学习强
- 受限于prompt tuning方法本身的限制。这一点作者做了用adpter找统一子空间的实验IST Adapter和用随机参数找子空间的实验(fine-tune相当于这个的d推广到所有参数),发现adpter的方法确实比pt更好
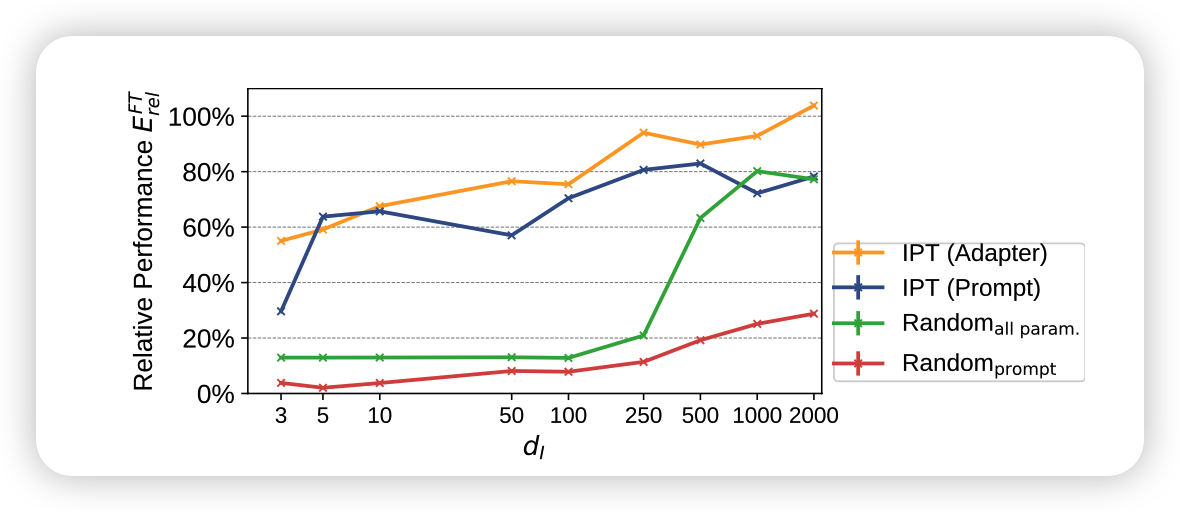
How is the influence of task types?
对比\(\mathcal{T}^{in}_{\text{test}}(\text{MSF}),\mathcal{T}^{out}_{\text{test}}(\text{MSF})\)可以说是惨不忍睹,说明生成任务和理解任务的差距还是非常远的
附实验
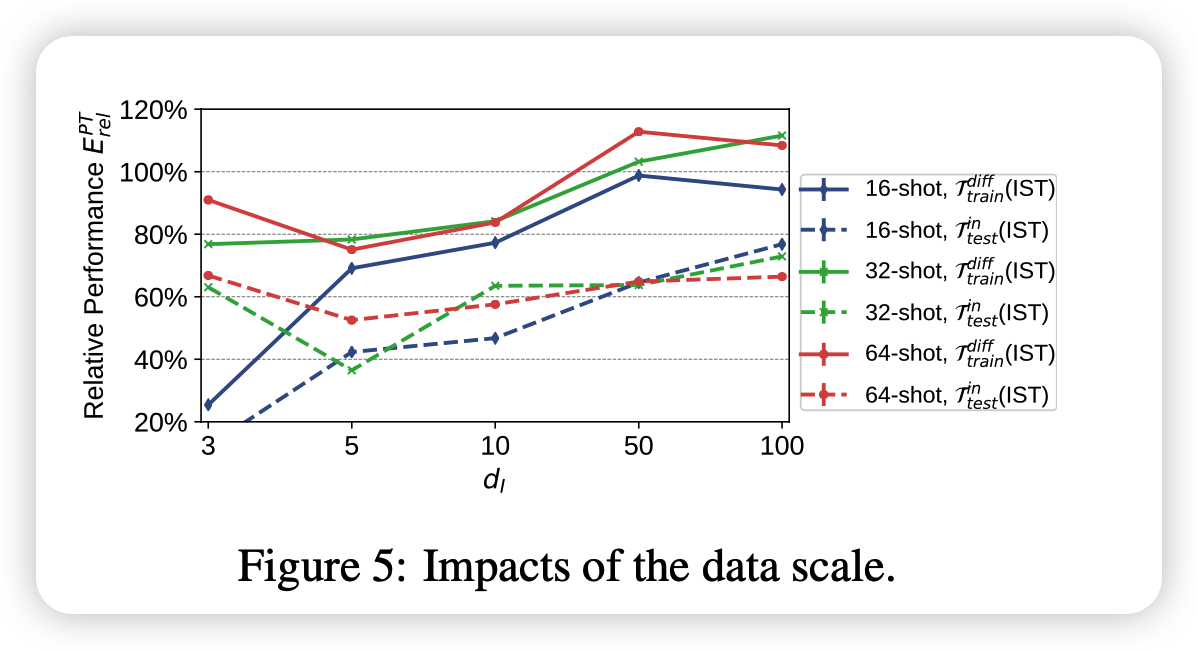
作者尝试增加训练集中的数据量,发现基本上就是数据越多,效果越好。当d小的时候增长更为明显
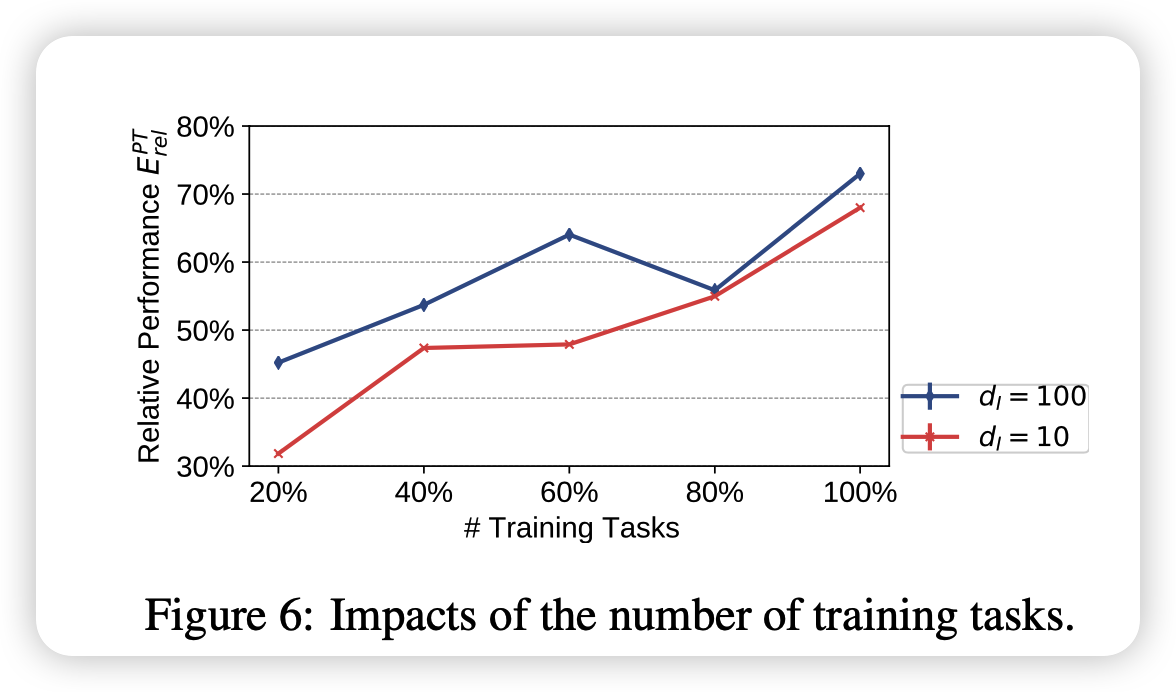
也探索了选用的可见任务多少带来的影响,说明可见任务越多,统一子空间的表征能力越强,或者说变换矩阵越准确
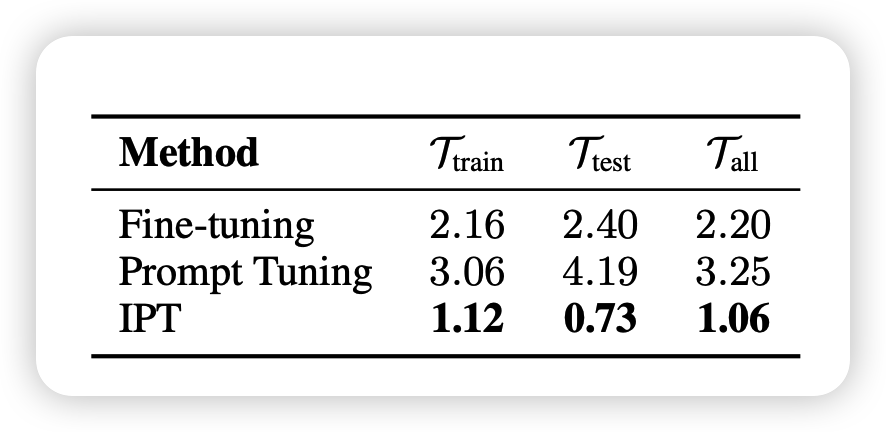
最后作者对比了稳定性,就是连续跑10次不可见任务每次score的方差:
- fine-tune的方差还行
- 直接做PT结果不稳定,或者说训练不好训
- IPT是指先用IPT PT跑出来一个soft prompt,然后作为起始点来进行真正的PT,这样结果最稳定。同时效果比单纯PT更强(103.4% \(E_{rel}^{PT}\))
因此从统一子空间出发更有利于PT训练的稳定性
我的思考
- 实验设计很精妙,想想作者的几个观点和对应的实验方法
- 所谓的统一子空间,有没有可能就是token空间?不知道是不是up sample出来的结果更接近于模型本身的某个word embedding
- 能不能结合预训练任务?比如说用预训练任务做proj, proj_b的训练,看看在下游任务能不能更好的进行低维表征