今天分享一篇上次adpter tuning的后文,进一步提升了效果、减小了参数量,发表在NeurlPS 2021上。了解这篇工作,需要先了解 Adpter Tuning笔记

本来以为作者是之前adpter的作者团队,结果发现竟然一个重合的都没有……
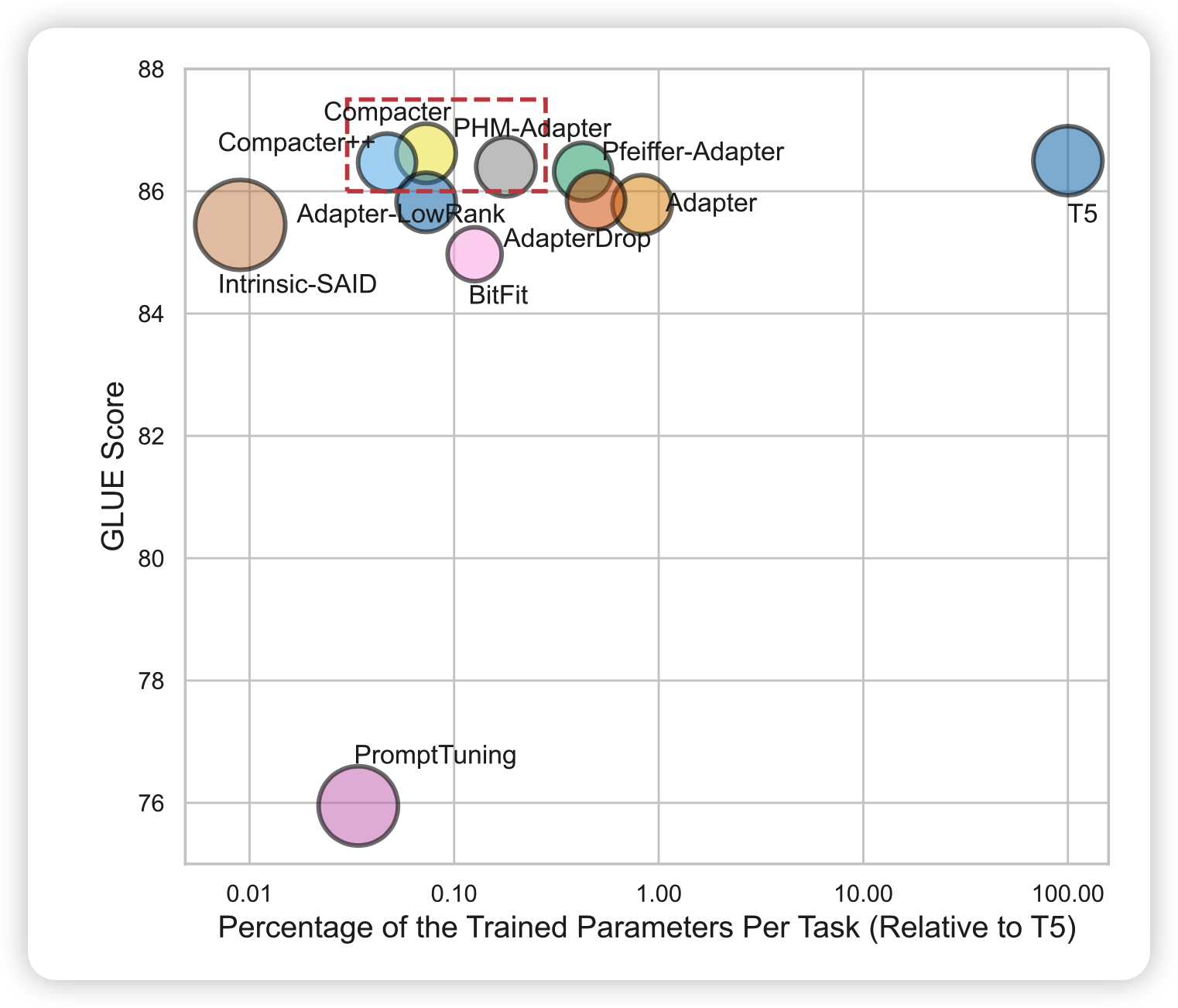
作者分析了一下已有的一些delta tuning方法和fine-tune。发现大多不如fine-tune好,作者想对adpter做一些改进,提升一下效果,减少一些参数。
方法
Kronecker Product
首先普及一下矩阵的Kronecker Product \[ A \otimes B = \left( \begin{array}{lll} a_{11}B & ... & a_{1f}B \\ & ... & \\ a_{m1}B & ... & a_{mf}B \\ \end{array} \right) \] 相当于把A的每一个元素都和B乘一下,然后\(A^{m\times f},B^{p\times q}\)就会变成\(mp \times fq\)的矩阵。注意,相当于用更少的参数表达了更大的矩阵
接下来,就是通过上面的方法来进行矩阵乘的优化
parameterized hypercomplex multiplication layers (PHM)

首先,作者想要达到全连接层的效果 \[ y^d = W^{d\times k}x^k + b \] 然后主要就是优化\(W\)
如果找到一个d,k的公约数n的话,\(W\)形状的矩阵可以视为 \[ W_j = \sum_{i=1}^n A_i \otimes B_i^j,\quad A\in \mathbb{R}^{n\times n},\quad B\in \mathbb{R}^{\frac{d}{n}\times \frac{k}{n}} \] 之所以要变成n个加在一起,好喜爱那个是为了增加自由度,让这个矩阵的表达能力和一个真正的大矩阵w的表达能力一样?
应用于adpter(LPHM)
为了用于实际的adpter tuning,其实就是就是把全连接层换了。同时作者还做了几个重要的修改:
- 所有的adpter层中,对于子矩阵A是共享参数的,这是为了更好的捕捉所谓的通用知识
- 然后每个adpter有单独的B,为了简化B的大小,可以把B变成秩更小的形式
\[ B^{m\times n} = s \times t^{T}, \]
s和t都是r个列向量,这样B的参数总共需要\(r\times(m+n)\)。这里的简化是基于上次adpter的实验中 单独的adpter层的影响很小 的结论,总而言之,最终的公式化简成了 \[ A^l(x)=\text{LPHM}^{U^l} (\text{GeLU}(\text{LPHM}^{D^l} (x)))+x, \] 作者对比了一下复杂度,发现和正常的adpter相比,可以把参数减少到大约\(\frac{1}{n}\)
实验
几个行的解释:
- compacter++:正常的adpter在每个transformer block加两次,这里探索只在最后的feedforward层后面加一次,就是比正常的参数更好
- PHM-Adapter:正常PHM矩阵乘的adpter,没有做A的共享参数,没有对B进行矩阵分解
- Intrinsic-SAID: 这个方式是想把模型的参数进行重参数化,然后需要用的额外参数非常少\(0.009\%\)。这个方法我后面可能也会做分享 Intrinsic Dimension笔记
- BitFit:和adpter另外的路子,只训练一些额外的bias,锁定正常参数
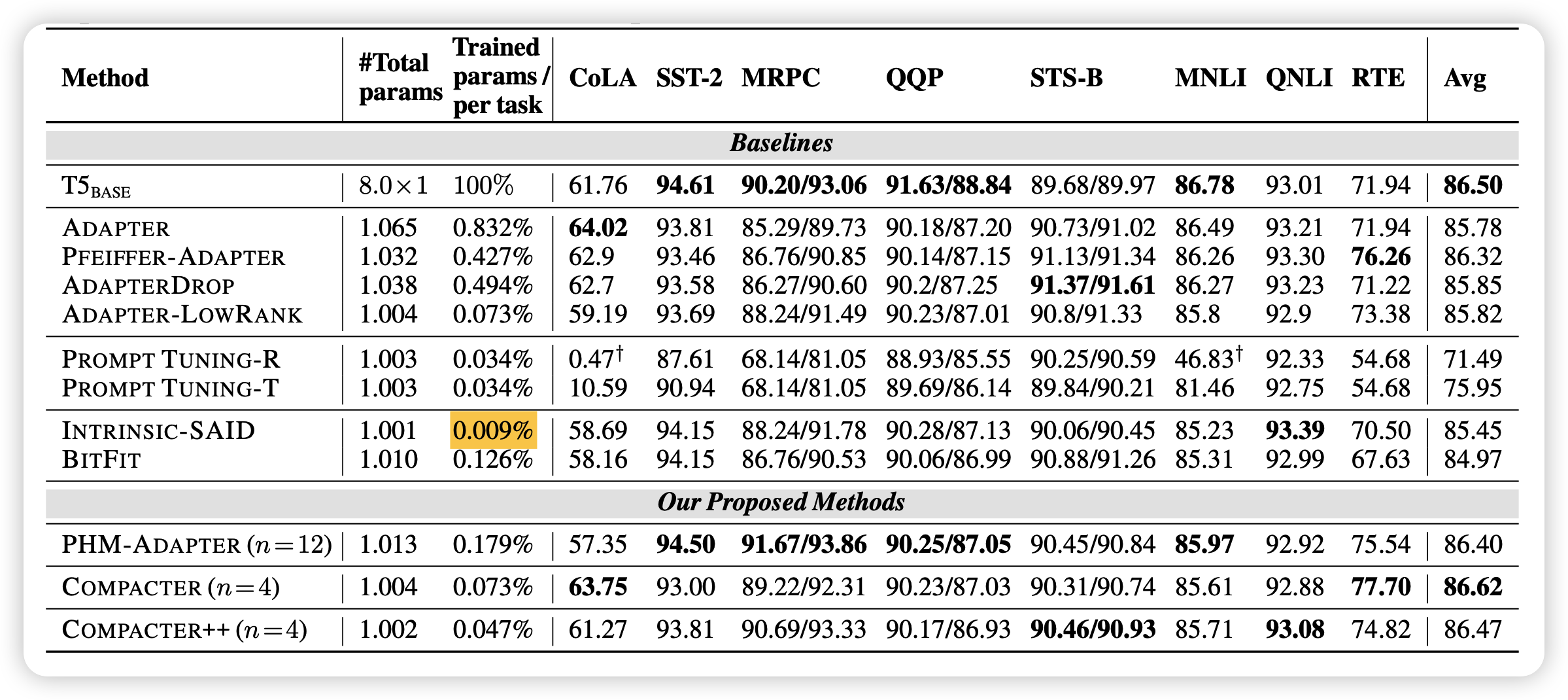
可以发现,作者对比了2021常见的几个方法,compacter方法最好:
- 发现共享A信息的compacter效果更好,这也说明了在不同adpter层间确实需要有一些共通的知识在
- 作者在实现中实际上用的B的分解秩r=1,这个好像并没有真的影响模型的效果
有一个好玩的点:
Intrinsic-SAID的效果甚至挺好的,参数还非常少,代价是什么呢?代价是训练时间长,以及对模型结构非常Aware
后面,作者直接显式地做了关于效率的附实验,有一些点就是:
- Intrinsic-ASID虽然参数少,但训练过程并不高效
- BitFit方法虽然效果稍差,但其实训练过程是很高效的

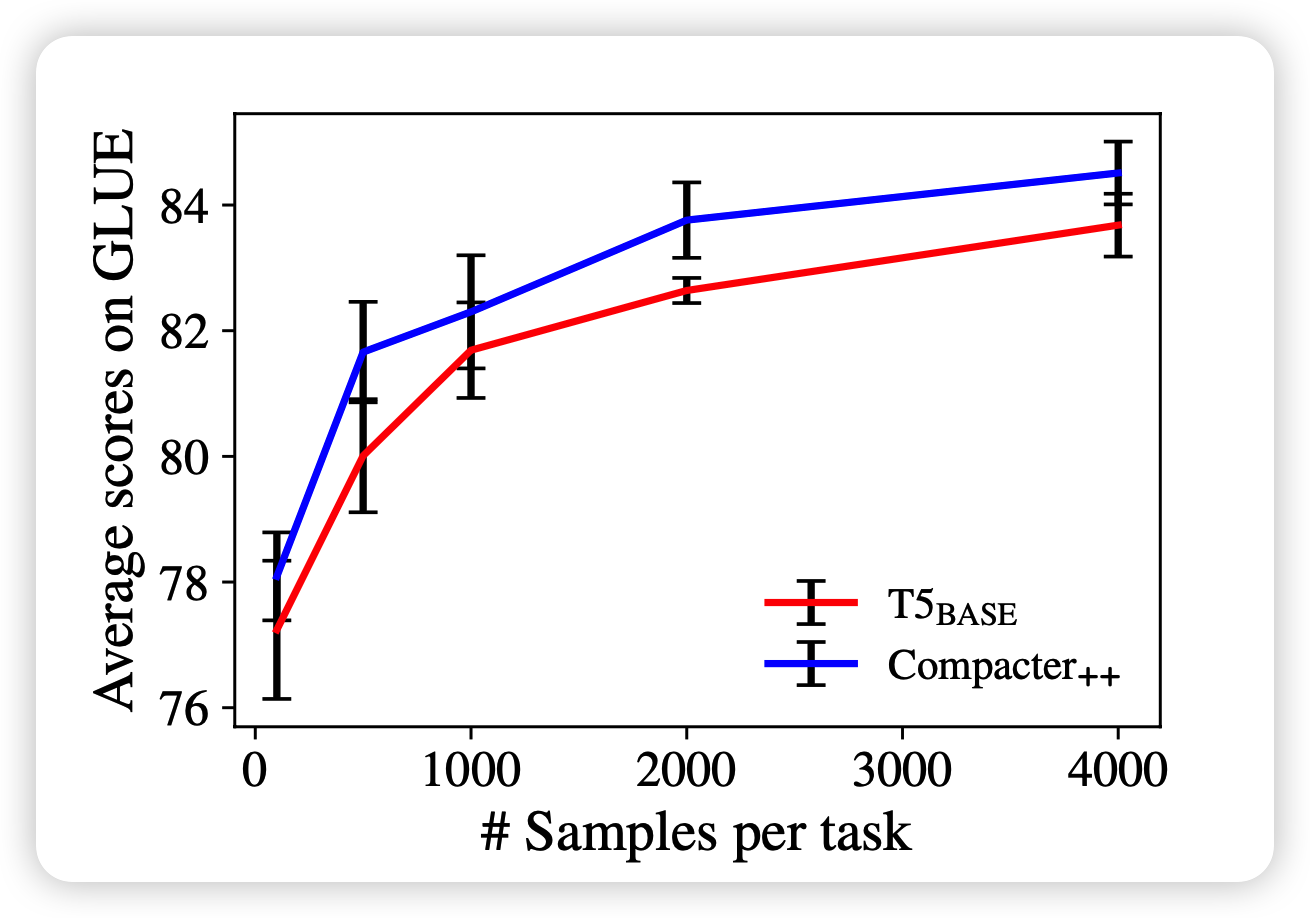
作者还额外提了一下,在少数据情况下,compacter比传统fine-tune的效果更好
我的思考
这个文章其实主要的idea还是沿用了adpter,但是思考通过优化矩阵乘的效率来减少参数很精妙,尤其是利用上了PHM共享A参数学习通用知识这个点,更是很妙。
我其实有几点好奇,文中没有说:
- B的分解秩r的大小对模型结果的影响。因为小的r显然会使得B的表征能力下降,但如果模型效果不下滑,是不是说明模型其实在下游中用到的知识真的是很少的?
- 模型高层和低层对应的B的影响的实验,参考正常adpter,因为这个实验的backbone模型是T5,之前是BERT。adpter提到的特性可以应用于其他的pre-train model吗?
- 单纯是否共享A参数的对模型效果影响的对比实验。如果这种层间通用知识真的有用,能不能在预训练阶段把模型结构就有所改进呢?
- compacter在少数据表现好的特性,是delta tuning共有的吗?因为我觉得其实delta tuning的上限就是fine-tune,所以超越fine-tune是不是代表,在这个下游任务上,现有数据集其实还没碰触到数据的边际效应递减