本来想写 Self-Consuming Generative Models Go MAD , 结果突然发现被苏老师抢发了,那就换一篇。
来讲讲软院去年ICML的Flowformer:如果把流图的思想引入到Attention算子中来。
这篇游神在知乎讲过一遍,我来主要分享一下在设计结构时我觉得比较好的一些思想,以及我对于线性attention的一些看法。
作者团队是软件学院

attention线性化
这篇文章中,主要讲了线性attention的问题。self-attention算子的一般计算是 \[ attn(x) = \text{softmax}(\frac{Q_x K_x^T}{\sqrt{d}})V_x \\ Q_x = Qx,K_x = Kx,V_x = Vx,\\ Q_x,K_x,V_x \in \mathbb{R}^{[batch,seq length,\text{hidden dim}/\text{head count}]} \] 其中最后一个维度是把原始的hidden state分成多个head,然后每个head分别计算attention,所以会除以 head count
这里就会发现,x的维度是[batch_size,seq_length,hidden_dim /head_count],所以整个计算的复杂度里对于seq_length这个维度是\(O(n^2)\)复杂度,当length很长的时候,这个是不能接受的
想想claude 2 的100k seq_length,来个 \(O(n^2)\)复杂度……
能不能把这个复杂度化简一下呢?这个问题就是学界一直在研究"attention线性化"的问题,但是往往复杂度下来了,效果也就下来了。
这里我们来一个思维实验,对于一个正常的LLM模型,比如说LLaMA

可以看到,65B模型,64个head,所以最后一个维度是\(8192/64=128\),是不是比seq_length小多了?我们再来看看原式子
如果没有这个softmax,我们的计算就大概是\(Q_x K_x^T V_x\),我们其实可以先算后面两个,变成一个 \(\mathbb{R}^{batch,128,128}\)维度的矩阵,再和Q相乘,一下子就变成针对seq_length的\(O(n)\)复杂度
所以说,这个\(O(n^2)\),就是因为非要算一个softmax?
softmax的过程可以看做对一个变换\(f: x_i, x_j \to y\in\mathbb{R}\)的结果进行竞争,这里取得核函数f是"点乘的e指数" \[ softmax(x)_{i,j} = \frac{e^{x_i*x_j^T}}{\sum_{x_k}(e^{x_i*x_k^T})} \] 其实,如果这个变换是可以分解的,也就是说是某个变化的点积 \[ f(x_i,x_j) = <\phi(x_i),\phi(x_j)> = \phi(x_i)\phi(x_j)^T \]
当然Q、K不一定用同一个变换函数\(\phi\),但道理是一样的
那么attention就是可以线性化的,用下面的式子化简: \[ \begin{aligned} attn(x_i) & = \sum_{j=1}^m \frac{f(Q_i,K_j)}{\sum_{j'} f(Q_i,K_{j'})} V_j \\ & = \sum_{j=1}^m \frac{\phi(Q_i)\phi(K_j)^T}{\sum_{j'} \phi(Q_i)\phi(K_{j'})^T} V_j \\ & = \frac{\phi(Q_i) * \sum_{j=1}^m(\phi(K_j)^T V_j)}{\phi(Q_i) * \sum_{j=1}^m\phi(K_j)^T} \end{aligned} \] 发现没,我们可以先花两倍的线性时间把\(\phi(Q),\phi(K)\)算出来,再花线性时间算出来$ _{j=1}m(K_j)T\(,再花\)O(nd2)\(时间把\)(K)TV$算出来
最后用线性时间就能把每个位置的attention算出来
一个最简单的想法就是:\(\phi(x_i) \equiv x_i\)恒等变化。然而,这样的话,\(f(Q_i,K_j)\)有可能是负的,这明显不可行
当然,这种变化需要保证仍然能满足softmax的一些性质,比如非负性、归一化、以及希望绝对值大的时候代表注意力高等等
之前苏老师提到了一种变换: \[ \phi(Q) = \text{softmax}_2(Q) \\ \phi(K) = \text{softmax}_1(K) \] 注意这里, K是在seq_length维度做归一化,Q是在d维度做归一化
可以发现,如果他们分别这样做了归一化以后,其实\(\phi(Q)\phi(K)^T\)天然就在seq_length维度上是归一化的
Flow Attention
其实上面提到的变换就和Flow Attention有点像了,在这篇工作中,作者思考了一个问题?
为什么要用softmax这个变换呢?
其实softmax是一种赢家通吃的竞争思路,尤其是在引入e指数以后,就更放大了这种"贫富差距"。
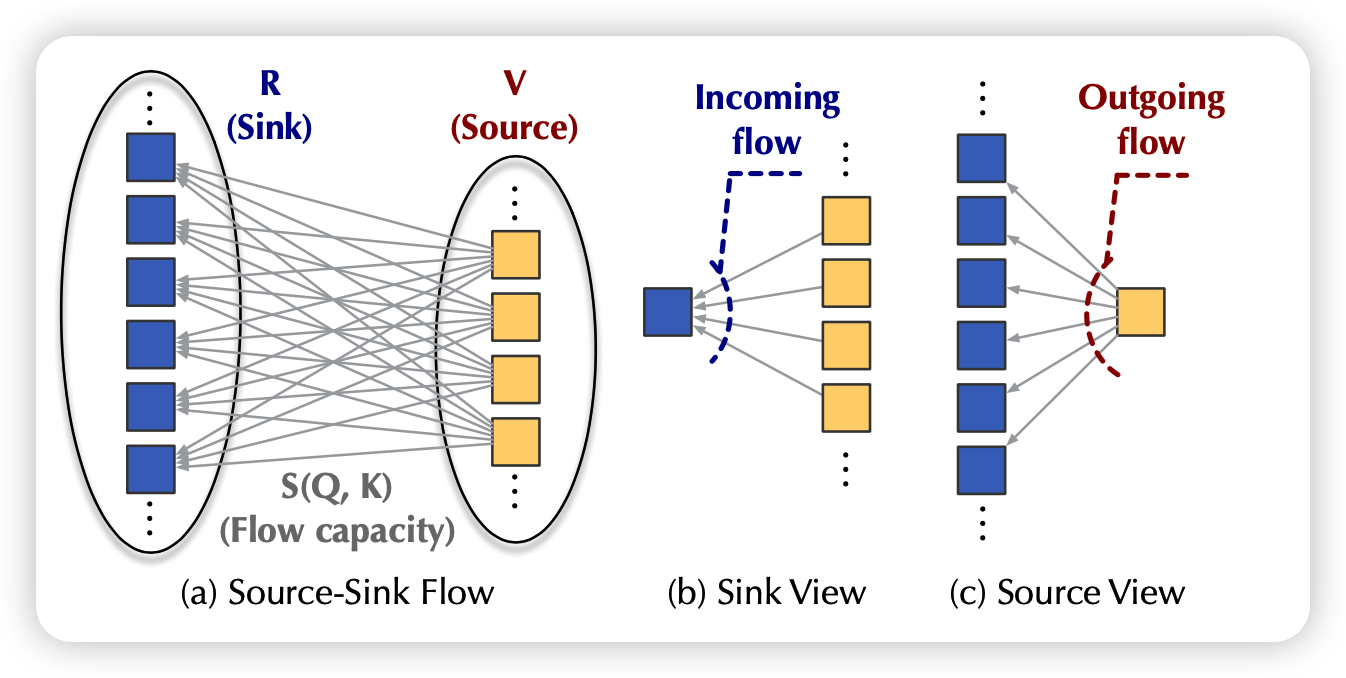
其实,流图就是一个天然的竞争场景,假如每层有m个源和n个池,两两之间都有一个流,因此所有池子的总流入量等于所有源的总流出量。
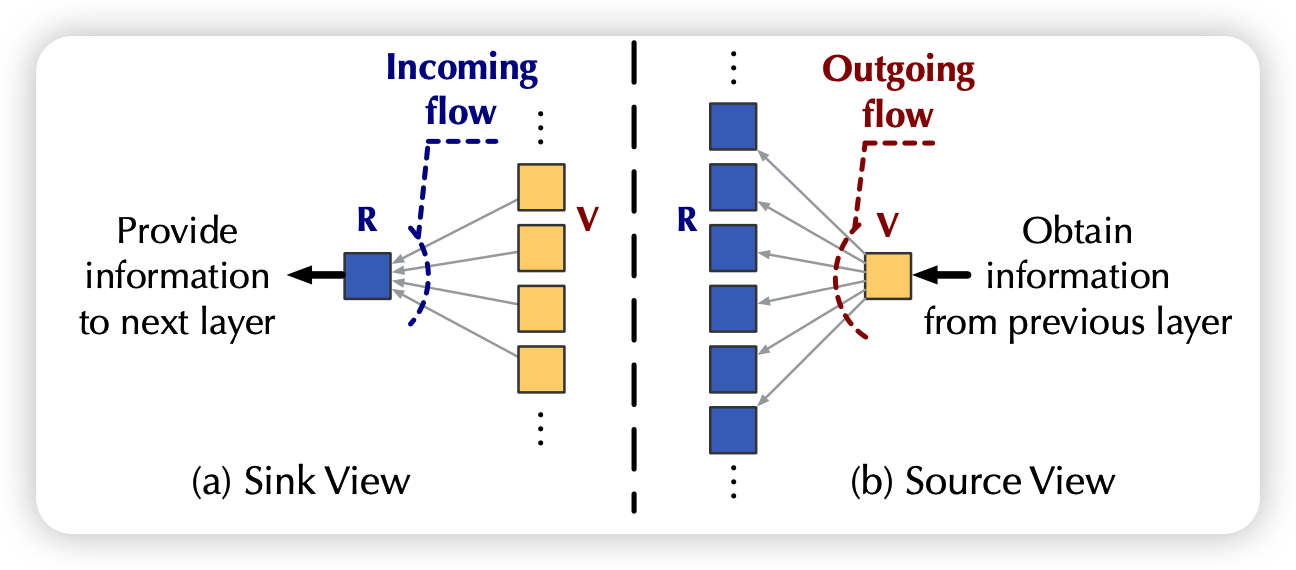
发现没,这时每个流的大小其实是天然符合attention定义的:注意力高就是流量大、天然的归一化、自带的竞争关系
作者就把流的计算方式定义成了乘积。K代表源,Q代表池子,从K流向Q: \[ \text{I}_i = \phi(Q_i) \sum_{j=1}^m \phi(K_j)^T \\ \text{O}_j = \phi(K_j) \sum_{i=1}^n \phi(Q_i)^T \\ \]
其中\(\phi\)变换保证变换结束以后每个元素都是恒正的
如果有很多层的话,其实上一层的池子就是下一层的源,一个简单的归一化方法就是要求每个节点: 流入量==流出量==1。作者就想了个归一化方法,除号是每个元素两两相除 \[ \frac{\phi(K_j)}{O_j}\quad \frac{\phi(Q_i)}{I_i} \] 此时,再来看流入流出量

这个恒1能保证,是因为要预计算所有的流量,然后求和再除回去
此时咱们来看流的大小 \[ \hat{I} = \phi(Q) \sum_{j=1}^m\frac{\phi(K_j)^T}{O_j} \\ \hat{O} = \phi(K) \sum_{i=1}^n\frac{\phi(Q_i)^T}{I_i} \\ \] 注意看,这个式子和上面的不一样 (求和的对象变了,所以不是恒等于1)
接下来,作者按照softmax的特性定义了三个操作
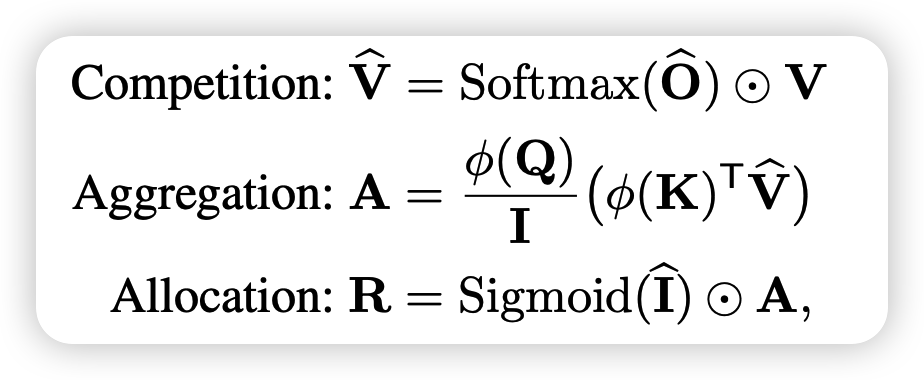
最后算出来的R就是attention的计算结果,这里面的哲学思想是这样:
- 竞争:每个V都是QK流竞争以后的结果
- 综合:A是每个源综合所有池子
- 申请:如果有某个池子的流很低,那么这个池子就抛弃,类似于之前说的"带1 softmax"
其中每一步操作都是线性的,综合的计算形式是这样:

实验部分就是把tranformer里的attention算子换成这个,然后在很多seq2seq下游任务上做了实验,发现效果都挺好
我的思考
flow attention方法虽然用流的思想包装了一下,但是计算形式其实和前面提到的双维softmax算起来比较接近。
他们都是为了解决所谓的"trival attention"的问题(attention矩阵变成所有位置都相同),因此要引入竞争。
我们从这个角度继续思考一下:softmax这个操作,其实是在每个元素自己向量的基础上,在向量间做了一个"归一化",然后再在Q K上分别做乘积。
一方面,我认为,这种思想甚至是不是能拓展到head之间呢?正常transformer是每个head内基本没有什么关系,是在attention算完以后再拼回去做变换。但其实head间也是可以竞争的,有些情况head1的结果更重要,有些时候head2的结果更重要。每个head在Q K V变换之前,以及attention的A矩阵计算之后,都是可以先拼再拆地计算结果,这样是不是可以让transformer的表示能力更强呢?
魔改版的MOE?
另一方面,我个人感觉transformer精巧的设计有三
- 一个是这里讲的竞争使得模型不会退化
- 另一个是先从低维的word dim变换成高维的hidden state再做head拆分,不丢失信息
- 最后一个是残差连接使得训练非常稳定