今天重新学习了一下reinforce/ppo上的loss形式，以及他们在反向传播时，实际对于lm_head层的梯度长什么样子。在2023年，我也写过一篇llm的ppo学习笔记，但当时其实我没有真的跑过大规模rl，对这个问题的理解远没有现在深入。2025年底，把这篇blog更新一下吧
Reinforce loss的推导(loss detrivative tricks)
从rl的初始，我们期待优化平均的reward的期望
\[ J = \mathbb{E}_{x \sim \pi_\theta}| R(x) | \]
显然，期望E是不可导的，这个公式J本身没有办法对\(\theta\)求梯度。怎么办，大家使用蒙特卡洛采样：
- 如果我在pi中采样一个batch的数据，这个数据上应该和目前的\(\theta\)是同分布的，我就在这个batch里优化
- 拿到一个batch的数据\(x_1, x_2, ..., x_n \sim \pi_\theta\)。每条数据有自己的reward。
\[J_i = x_i(\theta) = \sum_{\text{action j}} p_\theta(j) * R_i\]
其中\(\sum_{\text{action j}}p_\theta(j)\)代表目前的policy在整个动作空间中，生成这条样本的概率。
接下来，我们想要对 J 求导\(\nabla J = \sum_{\text{action j}} (\nabla p_\theta(j)) * R_i\)，问题在于：p是一个分布，一个分布本身是没有导数的。我们需要让公式右侧出现正常的p，而不是p的导数\(\nabla p\)
学界发现了所谓的"loss-derivative trick"，\(\nabla \log x = \frac{1}{x} * \nabla x\)
所以
\[ \nabla J = \sum_{\text{action j}} ( \nabla p_\theta(j)) * R_i = \sum_{\text{action j}} (p_\theta(j) * \nabla \log p_\theta(j)) * R_i = R_i * \nabla \log p_\theta * (\sum_j * p_\theta) \]
这种情况下，最右侧的sum就被蒙特卡洛替代了，我们直接在采样出的样本上，使用
\[\textcolor{red}{\text{loss}} = \log \pi_\theta * R\]
它的导数的期望，就和J的导数的期望是相同的，是对J的一个无偏估计。越大的btz，导数的方向就越准确
reinforce loss对lm_head层的所有参数的梯度数值
现在，我们脱离公式，思考模型结构，我们知道实际上的\(\pi_\theta\)，是从模型的lm_head层做了一次softmax得到的。由于sigmoid的梯度性质，可以推导出log softmax算子求导有一个很好的性质
\[\frac{\partial \log \pi_y}{\partial z_i} = \begin{cases} 1 - \pi_y & \text{if } i = y \text{ (是目标token)} \\ -\pi_i & \text{if } i \neq y \text{ (是非目标token)} \end{cases}\]
所以，假设z是lm_head层的输出的话，我们利用概率的性质，不对loss求导，直接看lm_head层的参数的梯度。这是一个矩阵，梯度也是分成两个部分：
- 采样到的token的行
- 剩余的所有行
我们先观察采样到的token的lm_head行向量参数的梯度:
\[ \frac{\partial loss}{\partial z_\text{采样到的token i}} = R * \frac{1}{\pi_\theta} * \frac{\partial \pi_\theta}{\partial z} = R * \frac{1}{\pi_\theta} * \frac{\partial \text{softmax}(z)}{\partial z} = R * \textcolor{red}{\frac{1}{\pi_\theta} * \pi_\theta} * (1 - \pi_\theta) = R * (1 - \pi_{\theta_i}) \] 神奇的现象出现了，\(\pi_\theta\)项被消掉了，这个梯度的数值非常稳定，不管pi本身特别接近0，还是特别接近1，他总是0-1之间。在lm_head层的每个参数，接收到的梯度精度很高(\(\pi_\theta\))，但数值范围永远很漂亮。
而剩余的没选中token的行向量的梯度则是： \[ \frac{\partial loss}{\partial z_\text{没采样到的、剩下所有的token j}} = R * (- \pi_{\theta_j}) \] 由于这些没选中的token，因为蒙特卡洛的性质，基本上\(\pi_{\theta_j} \sim 0\)，所以大家可以理解成没有梯度，或者说是一个非常非常小的、和reward方向相反的梯度。lm_head这一层的梯度全部集中在被选中的那个token上，且该token的概率越大，梯度就越小。
这里也可以看到softmax的另一个有趣的性质。如果把这一层的所有参数的梯度加起来，会发现他们正好sum=0。因为所有token的概率求和是1。softmax就是一个零和博弈
PPO，以及PPO为什么需要clip
接下来，我们开始讨论ppo算法。ppo假设我们使用过去的policy对梯度进行估计，此时为了保证\(\nabla J\)仍然对于\(\theta\)是无偏的，我们需要用统计学中的importance sampling方法 \[ \mathbb{E}_\theta = \mathbb{E}_{\theta_\text{old}} \frac{P_\theta}{P_{\theta_\text{old}}} \] 此时，假如我们用相同的方法观察ppo，不带clip版本时的loss，就变成了 \[ \text{ppo-loss}_\text{法外狂徒版} = \frac{\pi_\theta}{\pi_{\theta_\text{old}}} * R \] 用我们刚才reinforce时的方法，同样利用softmax的性质，推导一下这个ppo loss对于lm_head层参数的梯度，最终会得到 \[ \frac{\partial \text{ppo-loss}_\text{法外狂徒版}}{\partial z_\text{采样到的token i}} = \textcolor{red}{\frac{\pi_\theta}{\pi_{\theta_\text{old}}}} * R * (1 - \pi_{\theta_i}) \] 发现了吗，假如新旧policy完全相同时，ppo的梯度和reinforce的梯度是完全相同的，在数值上没有任何区别，等价。这不是巧合，是schulman精心设计出来的情况！但是，在采样policy和训练policy有区别时，就会产生出问题了。我们考虑两种极端情况：
- 当\(\pi_\text{old} \rightarrow 0\)，而\(\pi_\theta\)正常时。这会导致梯度爆炸，这一条数据中，lm_head层的参数突然收到了一个被放大1000、甚至10000倍的梯度，一下冲垮了之前整个训练时精心准备的梯度。
- 当\(\pi_\theta \rightarrow 0\)，而\(\pi_{\theta_\text{old}}\)正常时。这个情况，还好，因为参数梯度趋向于0。其实也就无所谓，白白浪费一条rollout...就当这条数据喂狗了
所以，ppo算法中需要加入一个clip机制。我这里⬇️直接使用了qwen最近这个工作里的公式，这和本身ppo那个很长的公式是等价的写法，看得更清楚一些。
\[
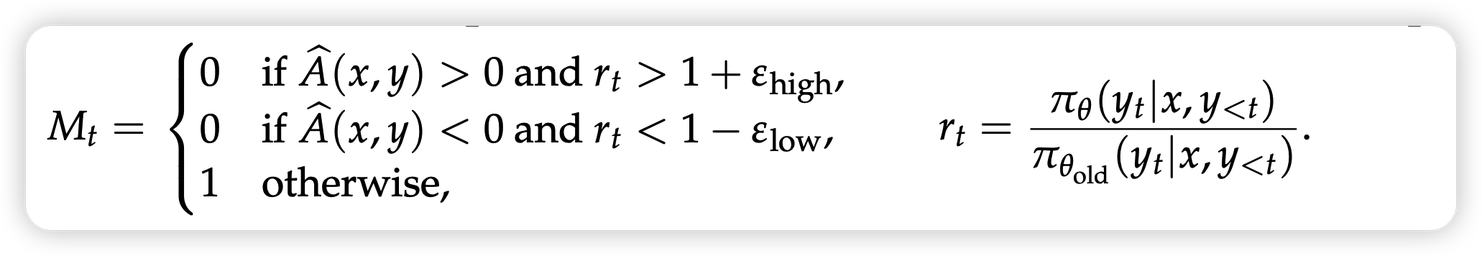\text{ppo loss} = \textcolor{red}{M}
*\frac{\pi_\theta}{\pi_{\theta_\text{old}}} * R
\] 从这个公式，我们重新分析我上面提到的两种危险情况：
- 假如\(\pi_\text{old}\)很小，后面变大了。往往是因为收到了正的reward，所以ppo设置了一个上界\(1 + \epsilon_\text{high}\)。超过阈值的token，根本不参与梯度计算
- 假如\(\pi_\text{old}\)后面变小了，就设置一个下界\(1 - \epsilon_{\text{low}}\)。
而在最近的deepseek v3.2的公式中，他们又额外加了一层保险，并且是在sequence level使用的
\[
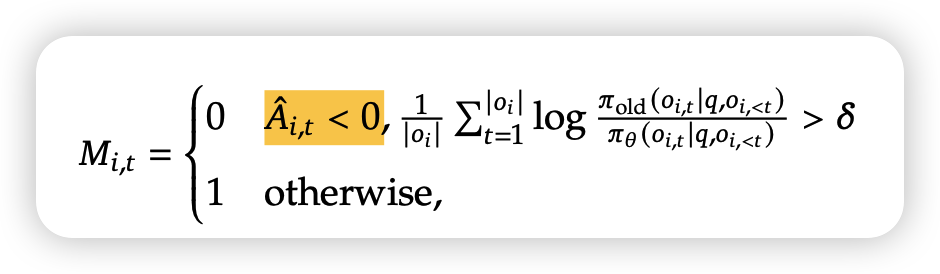\text{loss} = \textcolor{red}{M} * \textcolor{blue}{M_\text{deepseek}}
*\frac{\pi_\theta}{\pi_{\theta_\text{old}}} * R
\]
额外防了第三种意外情况：假如一个sequence里所有token平均上，\(\pi_\text{old}\)都很小，那干脆把这个sequence整体clip掉，不参与梯度计算
sft loss的梯度
其实，刚刚对lm_head层参数梯度的分析，是一个比较通用的方案。我们可以用这个方法再来分析一下pretrain/sft 这个cross entropy形式loss的梯度 \[ \text{sft loss} = -\log \pi_{\theta_\text{target}} = -\log \pi_{\theta_\text{target}} * 1 \] 相当于一个reward=1的rl训练， 并且\(\pi_\text{old}=\pi_\theta\)。所以，用一样的技巧分析他lm_head层的梯度 \[ \frac{\partial \text{sft-loss}}{\partial z_\text{target token i}} = (1 - \pi_{\theta_i}) \]
\[ \frac{\partial \text{sft-loss}}{\partial z_\text{other token j}} = (- \pi_{\theta_j}) \]
我们可以发现，由于没有importance sampling系数存在，无论本身模型生成target token i概率\(\pi_{\theta_i}\)大还是小，整体的梯度都比较稳定。当然，数值稳定，不代表数值就小。因为sft loss是在所有target token上计算的，如果模型本身生成一个token的概率很小，那么对应的lm_head层的梯度可就很大了。从数值上来说，sft loss的grad_norm一般比rl grad_norm大一个数量级。我们基本可以这样理解 \[ \text{grad-norm} \approx |\hat{A}|*(1 - \pi_{\theta_i})，其中|A|是\text{Mean Absolute Deviation} \] 对于sft loss，假如cross entropy=0.8，那么\(\text{grad}_{\text{sft}}\approx 1 - e^{-0.8}=0.55\)
对于rl loss，假设entropy \(H=0.2\)。那么\(grad \approx |\hat{A}|(1 - e^{-H})\)，我们假设
- 对rl advantage做了batch normalize。由于batch norm的数学性质，我们求出，此时的\(|\hat{A}| = \sqrt{\frac{2}{\pi}}\)
- rl中的entropy一般是单峰分布，也就是说top1 token几乎主导了entropy。此时可以直接用entropy代表\(\pi_{\theta_i}\)
在这个情况下那么\(\text{grad}_{\text{rl}} \approx 0.14\)
是不是和我们的实验结果差不多对应上了？